To find derivative of $x!$ W.R.T $x$

Question

I was curious to find the derivative of $x!$ and tried it myself on a basic level.

This is what I tried :- enter image description here (Please forgive me for not writing it in text I am bit slow in that and lazy too!)

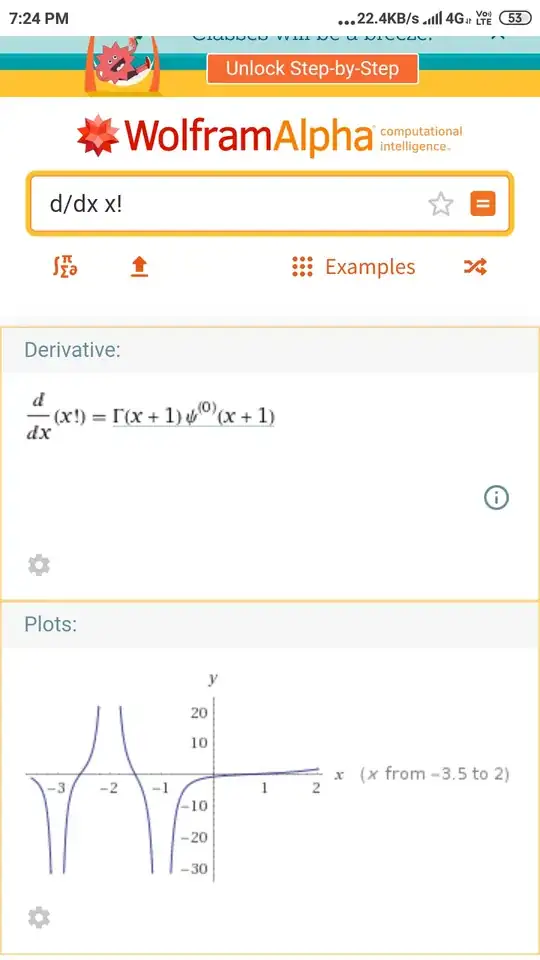
My question is whether this answer is correct or not since i find answers which are really beyond my knowledge:- enter image description here

Please help me figuring out whether my answer is correct or not and if correct then why wolfram shows such answer. (I am student and have no idea about those functions) Thanks!

Interpreting the question as whether or not that is the derivative of $\Gamma(x+1)$, the most common extension of the factorial, on natural arguments, the linked dupe provides the result. — Simply Beautiful Art, Sep 04 '19 at 17:23

score 2 · Accepted Answer · answered Sep 04 '19 at 17:13

The big problem with your answer is that you are working with the factorial function defined on the natural numbers. Such a function can't be differentiated so easily, as the standard definition of a derivative at a point requires the function to be defined in some open neighbourhood of that point. What wolfram alpha, and other sources I assume, are showing you is the derivative of the canonical extension of the factorial function to (most) of $\mathbb{R}$, the Gamma function.

Thanks for your answer I was searching for that only. – Akshaj Bansal Sep 04 '19 at 17:19 — Akshaj Bansal, Sep 04 '19 at 17:19

To find derivative of $x!$ W.R.T $x$

1 Answers1