Q1:
Funnily enough, while we rote learn this fact as we begin high school, it is seldom explained why this is the case. I will offer an intuitive explanation as well as a proof:
Negative numbers are commonly understood to have the opposite effect to positive numbers. If, as shown in the diagram, we establish the positive direction to mean steps to the right, then the negative direction is steps to the left. For example, adding 5 results in 5 steps in the positive direction. What then does adding -5 result in? It still results in 5 steps, but instead of going right, we go left. Left is the opposite of right, so "-5 steps to the right", as strange as it may seem, means "5 steps to the left". The '$-$' sign means 'opposite', so "-5 steps to the right" can be read as "the opposite of going 5 steps to the right", which is the same as "going 5 steps to the left". 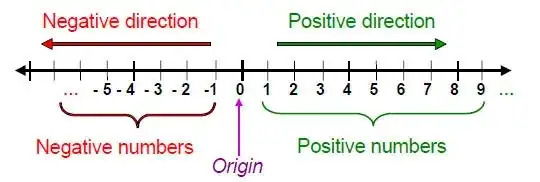
Image credit: https://brilliant.org/wiki/representation-on-the-real-line
What then does $-3$ times $5$ mean? We can take the easy route out and interpret this as "$5$ lots of $-3$", but how about we interpret it as "$-3$ lots of $5$"? Using our definition of negative meaning 'opposite', we can translate this as "the opposite of having 3 lots of 5", and the opposite of 'having' is 'owing'. Hence, it equals $-15$. Another way of thinking about it is with 'jumps' on the number line, a bit like the ones shown in the image below.  Image credit: http://www.homeschoolmath.net/teaching/md/division-repeated-subtraction.php
Image credit: http://www.homeschoolmath.net/teaching/md/division-repeated-subtraction.php
If we make $3$ jumps of length $5$ starting at 0 when we multiply $3$ and $5$, the jumps are going to the right. A 'negative' jump therefore is a jump to the left, at least in this case. $3$ of these negative jumps lands you at $-15$. And what about $-3\times-5$? In this case, multiplying $-5$ by a positive number results in steps to the left. If a 'normal' jump is to the left, then a negative jump is to the right. Imagine $2 \times -5$ as $2$ jumps to the left. $1 \times -5$ is a single jump to the left, $0 \times -5$ means no jumps, and $-1 \times -5$ is a single jump to the right (or, if you prefer, a "single jump opposite to the left"!). We are almost there; make 2 more of these negative jumps and you will reach $+15$. While this kind of reasoning is certainly not mathematically rigorous, it might provide a more user-friendly explanation than the textbooks offer.
Here is the proof:
- Let $a,b$ equal some positive real numbers
- $-a(-b+b)=0$
- $\Rightarrow (-a)(-b)+(-a)(b)=0$ (using the distributive property)
- Since we don't know what $(-a)(-b)$ is, let's replace it with $x$. Let $x = (-a)(-b)$
- $x-ab=0$
- $\Rightarrow x = ab$
Q2:
At first glance, the answer $a^2+b^2$ does seem to make sense. After all, $(ab)^2$ does equal $a^2b^2$. However, when rewriting the question in the long-hand form, the error becomes clear: $(a+b)(a+b)$ can't equal $a^2+b^2$ because the $a$ in the first bracket is multiplying both $a$ and $b$ in the second bracket (not just the $a$ in the second bracket on its own). Imagine $a=5$ and $b=7$ and instead of just multiplying $12$ by $12$, you wanted to work out in the general way: $(5+7)(5+7)$. Here, coming up with the answer $a^2+b^2$ would be akin to only multiplying the $5$ by $5$ and the $7$ by $7$, which gives you the wrong answer (try adding these up if you still don't believe me). It is clear that the $5$ and $7$ are also being multiplied together, two times in fact! (The outside and inside terms of the brackets are being multiplied). An easy way to remember which numbers to multiply together is the FOIL method: multiply the First terms together, then the Outside , Inside, and the Last ones. Add everything up and this will be your answer. Note: applying this to the general equation $(a+b)^2$ gives you a sneaky formula:
$$(a+b)^2$$
$$=(a+b)(a+b)$$
$$=a^2+ab+ab+b^2$$
$$=a^2+2ab+b^2$$
And here is a geometric proof (credit to Johannes for this visual from Visually stunning math concepts which are easy to explain):
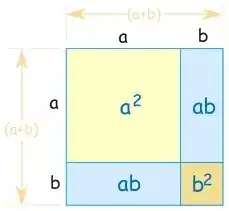
Note that $a$ could be smaller than $b$ – we are just using example lengths to prove the formula. This formula is extremely useful: imagine you didn't know your $12$ times tables, but knew your $10$ and $2$ times tables in a heartbeat. How could you work out $12 \times 12$? Sure, you could do $10 \times 12$ and then $2 \times 12$, but here is a method that bypasses the $12$ times table completely:
$$12^2 = (10+2)(10+2) = 10^2+2(10)(2)+2^2$$ Did you spot why this works? It still gives you the correct answer!
Q3:
The world of graph transformations is a confusing and counter-intuitive place, and this rule is no exception. However, as soon as you grasp its subtle internal logic, you will be instantly convinced as to why this rule is always true. To make the explanation clearer, let's make up some numbers and plot the graph $f(x)=3x+10$:
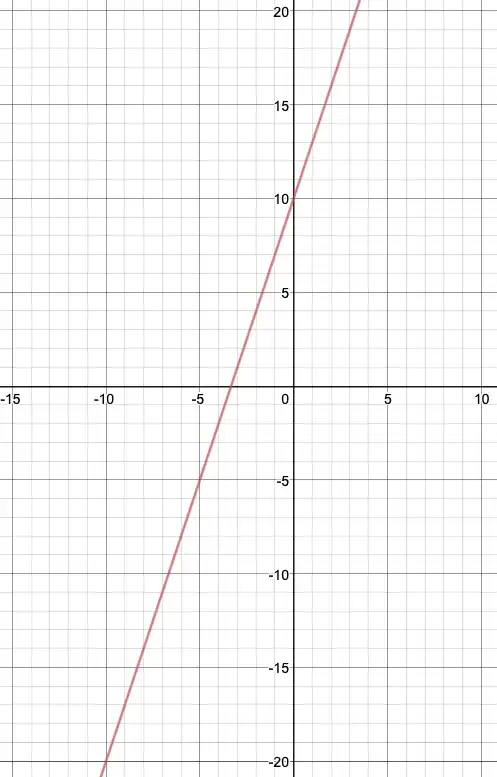
The graph $f(x+2)$ must therefore equal $3(x+2)+10$: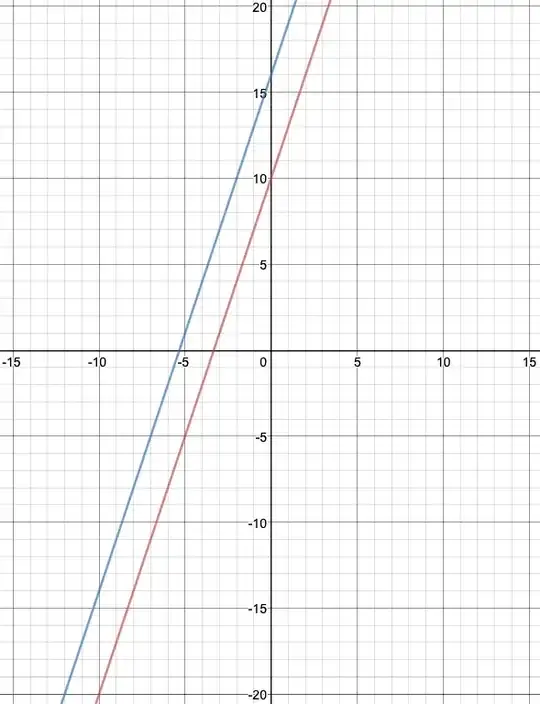
Take a look at these 2 graphs. If we inputted $x=3$ into my original, unshifted graph, what would be the output? $3(3)+10=19$, so $f(x)$ would equal $19$. What $x$-value would we have to input into my shifted graph to get $19$? Take a look at the graphs side by side if you can't work it out. That's right — we only need to input $x=1$ because the new, shifted graph is more 'powerful'. In other words, it can take smaller $x$-values and yet still get the same $y$-values, because it adds $2$ to the $x$-values before it does anything else. To be precise, we can input into my shifted graph $x$-values that are $2$ smaller, and yet still end up with the same $y$-values as before.
So why then is it so tempting to believe the graph shifts to the right and the left? I would it say it is a case of faulty intuition. It just seems to 'obvious' that we are just adding $2$ to the $x$-values, and everything else stays the same. However, if you remember that the $y$-values are being plotted against the $x$-values, and not anything else, then this argument falls apart.
I hope to answer more of these questions soon. Thanks for reading.




