impossible lengths of a train toy made by two types of wooden pieces.

Question

A train toy is made of a series of any number of wooden pieces, each piece is either 6 cm or 7 cm long. how can I -mathematically- prove that the train can never be 29 cm long?

Answer 1

Constructing a train out of 6- and 7-inch cars is equivalent to taking some number of 6-inch cars and then adding a number of 1-inch pieces no greater than the number of 6-inchers. That is, you want to find nonnegative integers $m$ and $n$ such that $6m+n=29$ and $m\ge n$. Clearly, $m\le4$, but what does this mean for $n$?

Answer 2

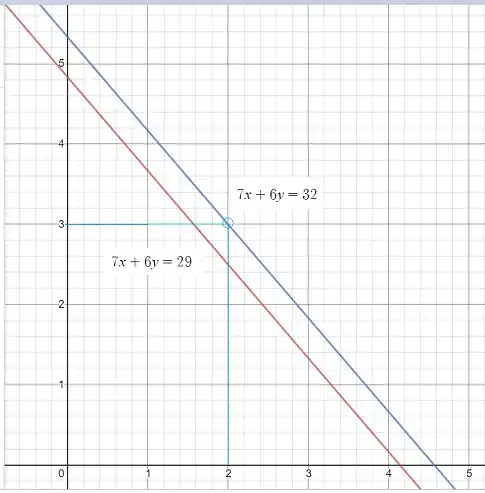
You could try to prove that the equation below (where $x, y$ represent the number of pieces of length $7,6$), has no integer solution for $x, y$ - Here we insist on integer values because the values represent pieces that have to be used as a whole and can't be cut to fit (at least I assume so):

$$7 x + 6 y=29 \tag1$$

If you don't want to get into number theory, and you don't want to try it by varying $x, y$, you can draw the line representing (1) (in this case it is the red one) You will notice that at the intersection of integer values of $x,y$, the point on the line is not an integer.

As an example of a case where you can find integer $x,y$ values, and how would they look like on the line graph, take the case of the Blue line provides a case where you can construct a train using $2$ pieces each of $7cm$ and $3$ pieces each of $6cm$.

To plot these lines you could do this:

1-Put $x=0$ to get the value of y-intercept

2-Put $y=0$ to get the value of x-intercept

3-Draw the line between the above $2$ points.