3

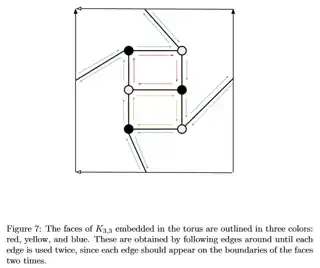
Due to Kuratowski's Theorem, graphs that contain the Utility graph as a subdivision can't be drawn in the plane. But on a genus $1$ surface, a torus! This is also resembled by Euler's characteristic: $$ \begin{array}{cCcc} \chi =& 2-2g &=& V-E+F\, \\ &0 &=& 6 - 9 \, \,+ \,3 \end{array} $$ We calculate $3$ faces! Now, I found at least two "flat" representations of the torus:

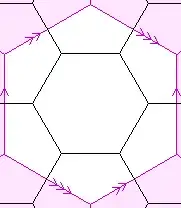
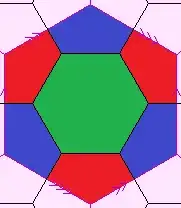
enter image description here $\hskip{2cm}$ enter image description here

To the left (the Lord and) I see two squares and one surrounding face and to the right it rather looks like three squares and a hexagon...

Why is that?

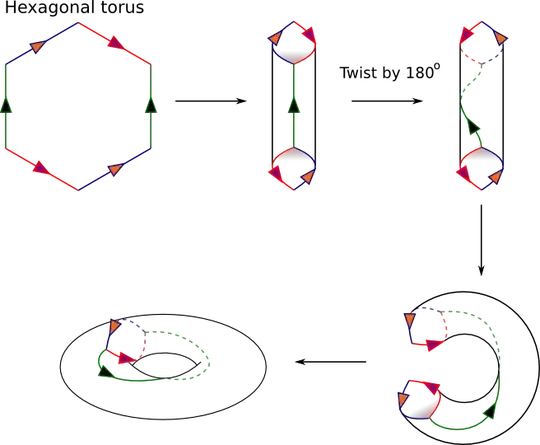
The hexagonal case needs another $180^\circ$ twist ("Indian Burn") to get the torus.

enter image description here

Is that relevant?

draks ...
  • 18,449

1 Answers1

3

Opps, I was wrong, with the right one. It just has two squares:

$\hskip{5cm}$enter image description here

To add something valueable, I found that the left torus is not strong embedded on the torus...

draks ...
  • 18,449
  • Can you please talk out what you mean by "strong embedded"? I was really taken in by your claim that there were four faces in that embedding, and even now that I understand that there are three, it still looks like that "external face" is adjacent to itself. I'm sure I could clear this up instantly if I owned a dry-erase torus, but I'm at the mercy of these diagrams. –  Aug 30 '19 at 09:45
  • @MatthewDaly from the linked reference: "Conjecture 1 (Strong Embedding Conjecture): Let $G$ be a $2$-connected graph. Then there exists an embedding of $G$ into a $g$-holed torus (for some $g$) such that the boundary of every face in the embedding is a cycle in $G$.

    You can see that the embedding we have given of $K_{3,3}$ (on the left) does not satisfy this requirement..."

     – draks ... Aug 30 '19 at 10:47