How many ways are there to define sine and cosine?

Question

Sometimes there are many ways to define a mathematical concept, for example the natural base logarithm. How about sine and cosine?

Thanks.

Answer 1

I like to define them by the differential equation:

$$y''=-y$$

and then, choosing the initial conditions we get these two functions. This also give rise nice definition for $\pi$ being the fundamental period for the solutions of these equations.

Answer 2

(This is by no means a comprehensive list.)

Right-triangle definition: the sine (cosine) of an acute angle is the ratio of the lengths of the leg opposite (adjacent to) the given angle to the hypotenuse of the triangle.

Bizarre Geometric Definition: the cosine of an angle in a triangle is $\frac{a^2+b^2-c^2}{2ab}$, where $a$ and $b$ are the lengths of the sides adjacent to the angle and $c$ is the length of the side opposite the angle; the sine of an acute angle is the cosine of its complement; the sine of an obtuse angle is the cosine of its supplement's complement. (edit: this one might be even worse than I'd originally thought as a definition, so perhaps just ignore it.)

Rotation-transformation definition: the sine (cosine) of a magnitude of rotation is the vertical (horizontal) coordinate of the image of the point (1,0) under a rotation of the given magnitude centered at the origin.

Unit circle definition: the sine (cosine) of a directed angle with vertex at the origin and initial ray on the positive x-axis is the y-coordinate (x-coordinate) of the point of intersection of the terminal ray of the angle with the unit circle centered at the origin.

Power series definition: $$\begin{align} \sin x&=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!}x^{2n+1}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots \\\\ \cos x&=\sum_{n=0}^{\infty}\frac{(-1)^n}{(2n)!}x^{2n}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots \end{align}$$

Exponential definition: $$\sin x=\frac{e^{ix}-e^{-ix}}{2i};\quad\quad\cos x=\frac{e^{ix}+e^{-ix}}{2}$$

Answer 3

An interesting construction is given by Michael Spivak in his book Calculus, chapter 15. The steps are basically the following:

$1.$ We define what a directed angle is. $2.$ We define a unit circle by $x^2+y^2=1$, and show that every angle between the $x$-axis and a line origined from $(0,0)$ defines a point $(x,y)$ in that circle.

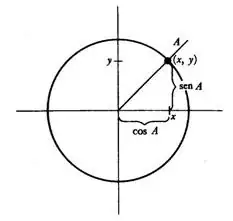
$3.$ We define $x = \cos \theta$ and $y = \sin \theta$.

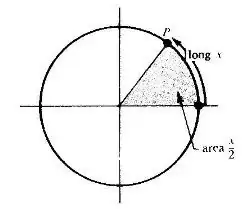
$4.$ We note that the area of the circular sector is always $x/2$, so maybe we can define this functions explicitly with this fact:

$5.$ We define $\pi$ as the area of the unit circle, this is:

$$\pi = 2 \int_{-1}^1 \sqrt{1-x^2} dx$$

$6.$ We give an explicit formula for the area of the circular sector, namely:

$$A(x) = \frac{x\sqrt{1-x^2}}{2}+\int_x^1 \sqrt{1-t^2}dx$$

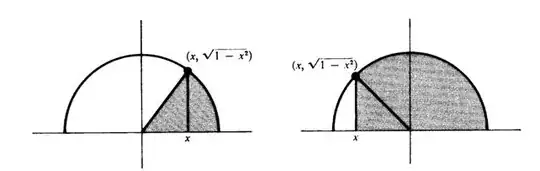
and show that it is continuous, and takes all values from $0$ to $\pi/2$. We may also plot it, since we can show that $2A(x)$ is actually the inverse of $\cos x$.

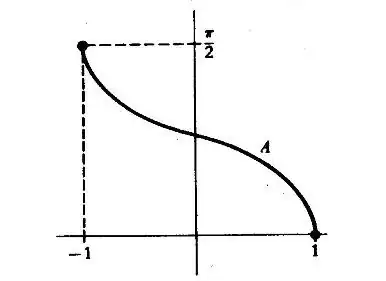
$7.$ We define $\cos x$ as the only number in $[-1,1]$ such that

$$A(\cos x) = \frac{x}{2}$$

and thus define

$$\sin x = \sqrt{1-\cos^2x}$$

$8.$ We show that for $0<x<\pi$

$$\cos(x)' = - \sin(x)$$

$$\sin(x)' = \cos(x)$$

$9.$ We finally extend the functions to all real values by showing that for $\pi \leq x \leq 2\pi$,

$$-\sin(2\pi-x) = \sin x$$

$$\cos(2\pi-x) = \cos x$$

and then that

$$\cos(2\pi k+x) = \cos x$$

$$\sin(2\pi k+x) = \sin x$$

Answer 4

I like good old definition using right angled triangle.

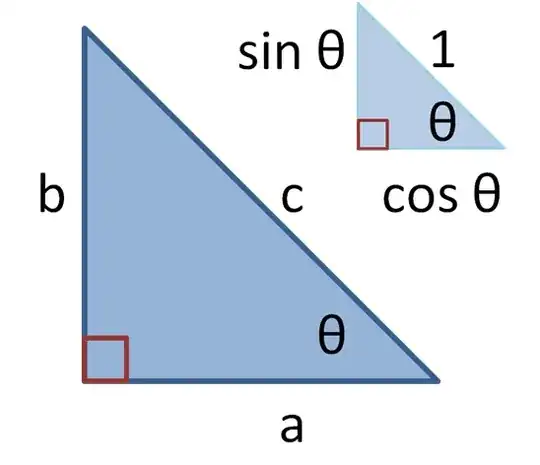
$$\sin\theta = b/c$$

$$\cos\theta = a/c$$

Answer 5

Once you define sine, you can define cosine to be the sine of the complementary angle. i.e. $\cos(\theta) = \sin(\frac{\pi}{2} - \theta)$. So you could reduce your question to asking for various ways of defining sine.

Answer 6

Try this:
http://www.wolframalpha.com/input/?i=sin

Click on all the "more"s - works of course for "cos" too!

Answer 7

It depends what you expect from the $\sin$ and $\cos$ functions.

Properties of $\sin$ and $\cos$ can be summed up by two functions $f$ and $g$ having following (simple) properties :

$$ f^2+g^2 = 1 \\ f' = g \text{ and } g'=-f \\ f''=-f $$

Now the question becomes in how many different ways a functions can be represented. Then you have the following list to begin with:

1. infinite series Power, Partial Fraction, Wesisentein, inverse factorials
2. infinite fractions
3. Fourier, Lagrange , Mellin etc. integral transforms
4. Infinite producs
5. Gamma, Beta functions, and other exotic functions

Now what you want to do is not to just focus on $\sin$ and $\cos$ in Euclidean Geometry, but what is sine of an angle on the sphere? tangent? cosine? what happens to them in a more general setting?

If you consider the functions by peridocity then this is what you want to look at: functional equations satisfying $f(x+k)=g(x)$. Then you can find even more interesting functions having double peridocity i.e. functions that $f(x+k_1)=g(x)$ , $f(x+k_2)=g(x)$ or $f(x+k_1)=f(x)$ and $f(x+k_2)=f(x)$ where $k_1\neq k_2$.

There are uncountable many ways to look for something that in special case would become the sine and cos we know from elementary days , for example if you use hypergeometric series then sin and cos are just special values of the hypergeometric series, but their properties satisfies what we needed from elementary sin and cos.

It is not the definition that matters but for what purpose they are being defined for, for example wit the infinite Power series nobody can see the periodicity and the infinite zeroes of the sin and cos, but with infinite Product representation (one still has to show the infinite series and the infinite product are the same thing), then it is obvious.

Answer 8

I think the following definitions are helpful in the sense they provide a reason to be interested in the numbers cos$(\alpha)$ and sin$(\alpha)$. These definitions show me what I can do with cosine and sine.

In a right angle triangle, $\alpha$ being the angle made by the hypothenuse and the adjacent side :

• cos$(\alpha)$ = the number by which you have to multiply the lenght of the hypothenuse in order to get the length the adjacent side

that is :

adjacent = hypothenuse $\times $cos$(\alpha)$

which is equivalent to the ordinary definition

cos$(\alpha) = \frac {adjacent} {hypothnuse}$

$\bullet$ In the same way , sin$(\alpha)$ is the number such that :

opposite = hypothenuse $\times $sin$(\alpha)$