3

Is $\mathbb{Z}[{ \sqrt 8 } ] $ a Euclidean domain ?

I have some confusion that is what is difference between euclidean domain and euclidean Norms ?

My attempt : I thinks yes

i know that $d( a+b \sqrt 8) = |a^2 - 8b^2 | $ as i can show it is euclidean domain by same pattern $\mathbb{Z}[{ \sqrt 2 } ]$ is euclidean domain

user26857
  • 52,094
jasmine
  • 14,457

3 Answers3

3

It is more straight forward to give a counter example. Since $4=2 \cdot 2 = (\sqrt{8}+2)(\sqrt{8}-2)$, $\mathbb{Z}[\sqrt{8}]$ is not a unique factorisation domain (UFD), hence not a Euclidean domain. Note that those factors are irreducible.

Suppose to the contrary that $2$ is not irreducible. There exists $a,b \in \mathbb{Z}[\sqrt{8}]$ with $N(2)=4=2 \cdot 2=N(a)N(b)$. It requires that $a,b \notin U(\mathbb{Z}[\sqrt{8}])$, the set of units. Therefore $N(a)=N(b)=2$.

Let $a=u+v\sqrt{8}$ with $u,v \in \mathbb{Z}$ and $u,v$ not both zero. It follows that $N(a)=|u^2-8v^2|=2$ $\implies$ $8v^2-u^2= \pm 2$. Therefore,

\begin{equation} (2v)^2 = \frac{u^2}{2} \pm 1 . \end{equation}

LHS is even. If $u$ is even, RHS is odd; a contradiction. If $u$ is odd, $ \frac{u^2}{2}\notin \mathbb{Z}$; another contradiction. Therefore $2$ is irreducible.

Note that $2 \nmid \sqrt{8} \pm 2$. Hence $\mathbb{Z}[\sqrt{8}]$ is not a UFD.

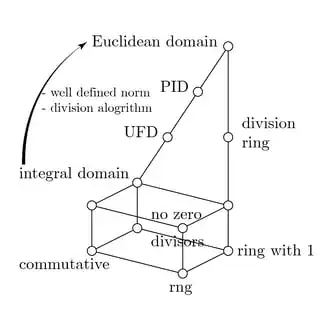
Hasse diagram from rng to ED

Link to a bigger image: Hasse diagram from rng to ED https://i.stack.imgur.com/jUcJX.png

Chan Tai Man
  • 182
3

Learn what the property "integrally closed" means and why every UFD is integrally closed. In particular, every Euclidean domain is integrally closed (Euclidean domains are UFDs).

The ring $\mathbf Z[\sqrt{8}] = \mathbf Z[2\sqrt{2}]$ is not integrally closed since $\sqrt{2}$ is in its fraction field and is integral over $\mathbf Z[\sqrt{8}]$ (being a root of $x^2-2$) without being in $\mathbf Z[\sqrt{8}]$. Therefore $\mathbf Z[\sqrt{8}]$ is not Euclidean or even a UFD, without having to give a specific counterexample to the UFD property: we showed this ring fails to have a property that every UFD (in particular, every Euclidean domain) satisfies: being integrally closed.

By similar reasoning, if $d$ is a squarefree integer and $m \geq 2$, then $\mathbf Z[m\sqrt{d}]$ is not integrally closed and thus can't be Euclidean (or a UFD).

KCd
  • 46,062
  • My background: I audited (i.e. not a proper maths student) an introductory abstract algebra course for ten weeks. I fail to understand what does it mean by integrally closed. These two wikipedia entires, Integrally_closed_domain and Integral_element, are too technical for me. Will you please point me to a more elementary explanation? Are you saying the problem is that $\sqrt{2}+\sqrt{2}+\sqrt{2} \notin \mathbb{Z}[2\sqrt{2}]$? Does it mean that it is not even a ring? Since addition operation is not closed, $+: \mathbb{Z}[2\sqrt{2}] \times \mathbb{Z}[2\sqrt{2}] \rightarrow \mathbb{Z}[\sqrt{2}]$. – Chan Tai Man Jan 26 '21 at 14:36
  • How $\mathbb{Z}[2\sqrt{2}]$ is different from $2\mathbb{Z}[\sqrt{2}]$? The textbook I use is R.B.J.T. Allenby (1991) Rings, Fields and Groups: An Introduction to Abstract Algebra. 2nd ed. Oxford: Butterworth-Heinemann. – Chan Tai Man Jan 26 '21 at 14:47
  • The term "integrally closed" is a rather technical property. It is not about an operation like addition not being closed or something not being a ring. Focus on understanding the answers other people gave. Come back to this answer after you have a better understanding of abstract algebra (not just from auditing a course). The notation $\mathbf Z[\alpha]$ means polynomial expressions in $\alpha$ with integral coefficients. In particular, $\mathbf Z[2\sqrt{2}]$ contains $1$ while $2\mathbf Z[\sqrt{2}]$ does not contain $1$, just like $\mathbf Z$ vs. $2\mathbf Z$. – KCd Jan 26 '21 at 15:10
  • Thanks. One last question. I did attempt to understand lhf's answer but without success. What is $v_\pi(2)$? – Chan Tai Man Jan 26 '21 at 16:36
  • Probably it means the highest power of a prime element $\pi$ that divides 2 (the $\pi$-adic valuation of 2). In $\mathbf Z$, $v_5(250) = 3$ since $250 = 5^3 \cdot 2$. – KCd Jan 26 '21 at 16:42
1

Every euclidean domain is a UFD.

Now, let $\alpha=\sqrt 8$. Then $2^3=\alpha^2$. If $ \mathbb{Z}[{ \sqrt 8 } ]$ is a UFD, we have${}^*$ $$2=\beta^2=(a+b\sqrt8)^2=(a^2+8b^2)+2ab\sqrt8$$ However, this equation has no solutions with $a,b \in \mathbb Z$. Therefore, $ \mathbb{Z}[{ \sqrt 8 } ]$ is not a UFD and so cannot be an euclidean domain.

${}^*$ $2^3=\alpha^2$ implies $3v_\pi(2) = 2v_\pi(\alpha)$ for every prime $\pi$. Then $v_\pi(2)$ must be even and so $2$ is a square.

lhf
  • 216,483