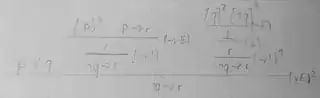Maybe it's easiest to grasp the difference between $\vdash$ and $\vDash$ by looking at some examples of what it looks like how to show each of them. As an example, let's consider $p \lor q, p \to r \substack{\vdash\\\vDash} \neg q \to r$ in classical logic.
A proof of $p \lor q, p \to r \vDash \neg q \to r$ looks something like this:
Consider the premise $p \lor q$. There are two cases to distinguish:
- Assume $p$ holds. Together with the second premise $p \to r$, since $p$ is true, $r$ must hold as well in order for the implication $p \to r$ to be true. If $r$ is true, then it is also true if $\neg q$, hence $\neg q \to r$.
- Assume $q$ holds. This is logically equivalent to $\neg \neg q$. All assignments which make $\neg \neg q$ will make $\neg \neg q \lor r$ true as well. By another logical equivalence, we have $\neg q \to r$.
Since $\neg q \to p$ follows from both cases, $\neg q \to r$ is true under all interpretations under which $p \lor q$ and $p \to r$ is true, therefore $p \lor q, p \to r \vDash \neg q \to r$.
or like this:
p q r p∨q p→r ⊨ q∨r
1 1 1 1 1 ✓ 1
1 1 0 1 0 1
1 0 1 1 1 ✓ 1
1 0 0 1 0 0
0 1 1 1 1 ✓ 1
0 1 0 1 1 ✓ 1
0 0 1 0 1 1
0 0 0 0 1 0
Since all the lines (≙assignments) under which all of the premises ($p \lor q$, $p \to r$) are true are also lines where the conclusion $p \lor q$ is true, $p \lor q, p \to r \vDash q \lor r$ holds.
A proof of $p \lor q, p \to r \vdash \neg q \to r$ looks something like this:

(natural deduction, Fitch (= linear) style)
or this:
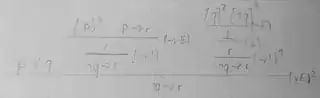
(natural deduction, Gentzen (= tree) style)
or this:
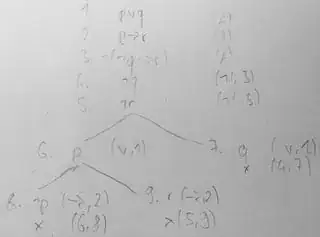
(tableau/truth tree)
Quoting mostly from this answer:
$\Sigma \vDash \Delta$ means that $\Delta$ is logically entailed by $\Sigma$, i.e., under all interpretations in which all of the premises $\Sigma$ are true, at least one out of the conclusions $\Delta$ is true. So here we're talking about the semantic notions of a language: Truth, assignment, interpretation, model. Rather than having precise rules that gets us from A to B by telling us which symbols to write where, we explicitly consider the truth conditions and argue why, by the meaning of the connectives, under all interpretations (in the case of propositional logic: = assignments; in the case of predicate logic: = structure) where the premises are true, the conclusion must be true as well. We can do this directly in the meta language with an English text, or, in the case of propositional logic, by looking at a truth table, where each line represents on assignment (= interpretation), or, when we want to show $\not \vDash$ in predicate logic, by presenting a countermodel, i.e. showing a structure (= an interpretation) which serves as a counterexample to the putative entailment. If we talk about truth, assignment, interpretation, model, then we talk about $\vDash$.
$\Sigma \vdash \Delta$ means that $\Delta$ is derivable from $\Sigma$ in some syntactic proof system. By "syntactic" we man a system purely operating on a set of rules that manipulate strings of symbols, without talking about semantic notations such as assignment, truth, model or interpretation. A syntactic proof system is one that says, for example, "If you have A written on one line and B on another line, then you are allowed to write the symbols A∧B on a line below that." Examples of syntactic proof systems are Hilbert-style calculi, sequent calculi and natural deduction in their various flavors or Beth tableaus aka truth trees. As you see in the three pictures above, at no point did we make explicit reference to things such as truth, assignment, interpretation: This is why it's called "syntactic": The rules only need strings of symbols in order to be applied, not their semantics (at least not explicitly). If we do a natural deduction, a tableau, a Hilbert-style proof, ..., then we talk about $\vdash$.
So $\vDash$ is about truth under some interpretations, and $\vdash$ is about derivability in some rule system.
As for the relation between the two:
Soundness ,
If $\Sigma \vdash \Delta$, then $\Sigma \vDash \Delta$
tells us that if we found a syntactic derivation, then we know that the entailment holds semantically. So if we have a natural deduction, tableau, ... proof of $p \lor q, p \to r \vdash \neg q \to r$ like in the first three pictures, soundness allows us to conclude that this is proof that the entailment relation holds according to the semantics of the language, $p \lor q, p \to r \vDash \neg q \to r$. Soundness is not too surprising: When a syntactic derivation system is defined, then reasonably it will be designed such that it properly reflects the semantics of the language, otherwise there's not much point in inventing such a system at all; and proving soundness is relatively easy (you just do induction on the rules and show that each of them are semantically sound).
Completeness,
If $\Sigma \vDash \Delta$, then $\Sigma \vdash \Delta$
tells us that if a semantic entailment holds, then we can find a syntactic derivation. So if the entailment $p \lor q, p \to r \vDash \neg q \to r$, $p \lor q, p \to r \vdash \neg q \to r$ holds by the semantics of the logic, then we know that we must be able to find a syntactic derivation $p \lor q, p \to r \vdash \neg q \to r$ in the syntactic system like natural deduction, tableaus etc. Completeness is non-trivial (the proof is much more difficult), and a very powerful result, as elaborated in in the answers to the question linked above.