4

$f(x)=ax^4+bx^3+cx^2+dx+e$

$a, b, c, d, e \in\mathbb{R}$

Suppose $f(x)=1$ has p distinct real solutions, $f(x)=2$ has q distinct real solutions, $f(x)=3$ has r distinct real solutions, $f(x)=4$ has s distinct real solutions.

Why is it not possible for $p=1, q=3, r=2, s=4$?

How can you tell that it's not possible for $p=1, q=3, r=2$, and $s=4$? I am stuck on this problem.

Community
  • 1
Eris Tyenns
  • 133
  • 1
    In essence, when $f(x)=e$, set $x=0$ and you have the $y$-intercept, in this case $y$-int=$1-e,2-e,3-e,4-e$ in that order. Well when you shift the $y$ intercept by $1$ each time, you should get a certain order of solutions. First, one solution, second two solutions, a third time three solutions, and a fourth time four solutions to this quartic equation. The order listed violates this rule. Thus it is an impossibility. – JohnColtraneisJC Aug 20 '19 at 17:47
  • Is it then possible for p=1, q=4, r=3 and s=2? The problem says that is it possible – Eris Tyenns Aug 20 '19 at 17:52
  • 1
    @ErisTyenns yes, the example in your comment is possible, something similar to https://www.wolframalpha.com/input/?i=plot+x%28x-1%29%28x-2%29%28x-3%29%3D0 – dcolazin Aug 20 '19 at 17:55
  • Ok, thanks. But I'm still lost, what's the difference between the numbers in my post and the numbers in my comment? – Eris Tyenns Aug 20 '19 at 17:57

3 Answers3

2

Since $f(x) - 1$ has only one root and all coeficients are in $\mathbb{R}$, we have only two cases to consider:

Case 1. $f(x) - 1 = a(x - \alpha)^4$

In this case, the function obtained is convex (if $a > 0$) and concave otherwise. In particular, it does not have any horizontal line that crosses it $3$ times.

Case 2. $f(x) - 1 = a(x - \alpha)^2 g(x)$ with $g(x)$ without real roots.

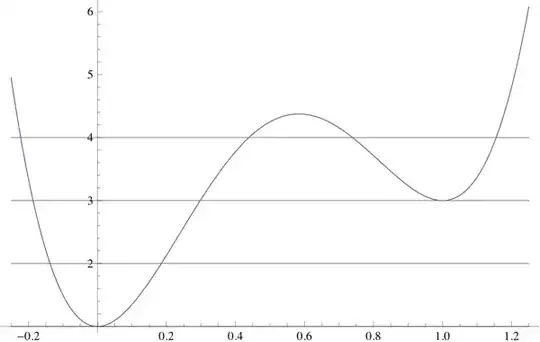
Here, we have to use the other data. Since there is a horizontal line that crosses the function $4$ times, we know it must have $3$ local maxima or minima. Also, since the $4$ roots happen at line $y=4$, we know that $a > 0$ and also $g(x) > 0$, that is, the function is always above line $y=1$ (hitting it at point $x = \alpha$). This already provides a very precise picture of the shape of function $f$. If you start with line $y=0$ and begin moving it upwards, the number of roots changes in this sequence:

$$0 \to 1 (\text{at } y=1) \to 2 (\text{immediately after})\to 3 (\text{local min})\to 4 \to 3 (\text{local max}) \to 2 (\text{immediately after}).$$

Notice that this sequence does not have $1 \to 3 \to 2 \to 4$ as a subsequence.

D. Ungaretti
  • 2,668
1

Consider $f$ a polynomial of degree $4$, then its derivative is a polynomial of degree $3$, so it has at most three critical points. There are only two cases.

First case: localmin-localmax-localmin (or max-min-max). The plot you have to imagine is this one. If you count the roots from the global minimum upwards you find $1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 3 \rightarrow 2$. But you can't find a subsequence $1\rightarrow 3 \rightarrow 2 \rightarrow 4$ in the roots number so it isn't possible. (And you can find $1\rightarrow 4 \rightarrow 3 \rightarrow 2$ as a subsequence). There are some details missing (what if the two min are at the same height?), but the core idea is here.

Second case: inflection point-min-inflection point (or flex-max-flex). The argument is the same as the first case.

dcolazin
  • 2,242
1

If one doesn't count multiplicities of roots $$ f(x)=36x^4-76x^3+42x^2+1 $$ has one point at which $f(x)=1$, two points at which $f(x)=2$, three points at which $f(x)=3$, and four points at which $f(x)=4$.

enter image description here

robjohn
  • 345,667
  • I misread the order of the number of solutions, but if we look at this image, we see the shape of one possible quartic: two local minima and one local maximum. Another type has just one local minimum and no local maxima. Both of these go to $+\infty$ as $x\to\pm\infty$. The negative of these have two local maxima and one local minimum or one local maximum and no local minima. Both of these go to $-\infty$ as $x\to\pm\infty$. – robjohn Aug 20 '19 at 21:16
  • If we have only one point at which $f(x)=1$ and four points at which $f(x)=4$ we must have the first type, the type shown above. In that case, to have three points at which $f(x)=2$, we must have four points at which $f(x)=3$. – robjohn Aug 20 '19 at 21:20