I need to find the roots for this function $$~ 2x - \tan(x)=0~$$ in order to graph it.
I have found the one root $~(x=0)~$ but there are two more $~(x= -1.164 ,~ x= 1.164)~$. How can I find these answers without a graphing calculator ?
Or is this not possible without a calculator?
Thanks, any help is appreciated.
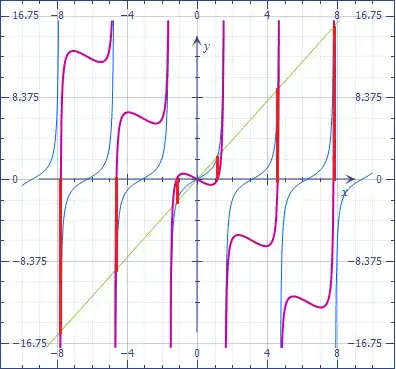
Consider that you look for the zero of function $$f(x)=2x-\tan(x)$$ and forget the trivial solution $x=0$. On the other hand, if $x$ is a root $-x$ is a root too. Then, we need to focus on the positive solution.
In the restricted interval, the derivative $f'(x)=2-\sec ^2(x)$ cancels when $x=\frac \pi 4$ which is a local maximum. So, to get an approximation, build a Taylor expansion around this point and get locally $$f(x)=\left(\frac{\pi }{2}-1\right)-2 \left(x-\frac{\pi }{4}\right)^2+O\left(\left(x-\frac{\pi }{4}\right)^3\right)$$ Ignoring for the time being the higher order terms, the approximation is then $$x=\frac{\sqrt{\pi -2}}{2}+\frac{\pi }{4}\approx 1.31962$$ which is not fantastic.
Adding one extra term to the series expansion would give $$f(x)=\left(\frac{\pi }{2}-1\right)-2 \left(x-\frac{\pi }{4}\right)^2-\frac{8}{3} \left(x-\frac{\pi }{4}\right)^3+O\left(\left(x-\frac{\pi }{4}\right)^4\right)$$ which can be solved using Cardano method. The solution would evaluate as $x \approx 1.21193$ which is better.
Now, to really polish the root, as said in comments, a numerical method is required and Newton method will be the simplest. Starting from the first estimate, the iterates would be $$\left( \begin{array}{cc} n & x_n \\ 0 & 1.31962 \\ 1 & 1.23096 \\ 2 & 1.17860 \\ 3 & 1.16612 \\ 4 & 1.16556 \end{array} \right)$$
Edit
You could have an approximation using a table lookup since we know the exact trigonometric functions for multiples of $\frac \pi {24}$ (see here). The closest value would be $x=\frac {3\pi} {8}\approx 1.17810$.
Let us repeat the Taylor expansion around $x=\frac {3\pi} {8}$ to get $$f(x)=\left(\frac{3 \pi }{4}-\cot \left(\frac{\pi }{8}\right)\right)+\left(x-\frac{3 \pi }{8}\right) \left(1-\cot ^2\left(\frac{\pi }{8}\right)\right)+O\left(\left(x-\frac{3 \pi }{8}\right)^2\right)$$ and use $\cot \left(\frac{\pi }{8}\right)=1+\sqrt 2$
This will give, as a better estimate, $$x=\frac {3\pi} {8}+\frac{1}{8} \left(3 \left(\sqrt{2}-1\right) \pi -4\right)\approx 1.16608$$
We could even do better using the simplest $[1,1]$ Padé approximant to get $$x=\frac {3\pi} {8}+\frac{4 \sqrt{2}+3 \left(\sqrt{2}-2\right) \pi }{8-6 \pi }\approx 1.16557$$
Edit
Since @robjohn gave the value of many solutions outside the range, considering that the $n^{th}$ positive solution $x_{(n)}$ is closer and closer to $(2n+1)\frac \pi 2$, I let $x_{(n)}=(2n+1)\frac \pi 2-\epsilon$ and developed the initial equation as a Taylor series around $\epsilon=0$. Then, using series reversion we get $$\color{blue}{x_{(n)}=q-\frac{1}{2 q}-\frac{5}{24 q^3}-\frac{83}{480 q^5}-\frac{2407}{13440 q^7}-\frac{856715}{4128768 q^9}+O\left(\frac{1}{q^{11}}\right)}$$ where $\color{blue}{q=(2n+1)\frac \pi 2}$.
For the first solutions, the table below gives the approximation from the above formula as well as the solution obtained using Newton method. $$\left( \begin{array}{ccc} n & \text{approximation} & \text{solution} \\ 0 & 1.16949833499836 & 1.16556118520721 \\ 1 & 4.60421678800531 & 4.60421677720058 \\ 2 & 7.78988375118261 & 7.78988375114457 \\ 3 & 10.9499436485421 & 10.9499436485412 \\ 4 & 14.1017251335659 & 14.1017251335659 \\ 5 & 17.2497818346079 & 17.2497818346079 \\ 6 & 20.3958423573092 & 20.3958423573092 \\ 7 & 23.5407082923052 & 23.5407082923052 \\ 8 & 26.6848024909251 & 26.6848024909251 \\ 9 & 29.8283692130955 & 29.8283692130955 \end{array} \right)$$
There is a far simpler method which does not involve calculus and which can reliably solve many equations of this kind. It does need a calculator, but not a graphing one.
Consider the graphs of $\tan x$ and $2x$ at the point of intersection near $\pi$. The tangent curves upwards while the linear function is a straight line.
In these circumstances, any estimate $x_0$ of the root of the equation will always be improved if you change it to $x_1=2\tan^{-1}x_0$. On the iPhone’s calculator this requires three keystrokes for each iteration. Repeating it moronically until the answer stops changing, one gets $$x=1.165561185207211$$
Whenever you have the right curvature of the intersecting graphs, this method will work. You need to decide which function to iterate, in this case whether $2\tan^{-1}x$ or $\frac12\tan x$, which you can do by sketching, by reasoning about curvature, or just trying it both ways and seeing which one converges and which one explodes.
Since the convergents are alternately too high and too low, you can accelerate a slow convergence by averaging the new value with the old one at each step.
And yes, you can justify the soundness of this method with calculus. But the method itself is independent of it and comes into its own in cases where the functions concerned are hard or complicated to differentiate.
Since the slope of $\tan(x)$ can be big, $2x=\tan(x)$ is not stable over a large domain. $\arctan(2x)=x-k\pi$ offers more stability; i.e. better convergence.
Newton's Method gives $$ x_{n+1}=\frac{(\arctan(2x_n)+k\pi)\left(4x_n^2+1\right)-2x_n}{4x_n^2-1} $$ When $k=0$, we get three attractors, depending on $x_0$. If $-\frac12\lt x_0\lt\frac12$, then $x_n\to0$. If $x_0\gt\frac12$, then $x_n\to1.1655611852072113068$. If $x_0\lt\frac12$, then $x_n\to-1.1655611852072113068$.
Table of Positive Solutions
Starting at $x_0=1$: $$ \begin{array}{c|c} k&\lim\limits_{n\to\infty}x_n\\\hline 0&1.1655611852072113068\\ 1&4.6042167772005765146\\ 2&7.7898837511445727737\\ 3&10.949943648541159333\\ 4&14.101725133565873243\\ 5&17.249781834607895990\\ 6&20.395842357309167481\\ 7&23.540708292305150112\\ 8&26.684802490925067321\\ 9&29.828369213095504277 \end{array} $$
DLMF function
Here is a closed form using “zeros of the Bessel function derivative” from DLMF defined by:
$$\frac{d\text J_n(x)}{dx}=\text J’_n(x)=\text J_{n-1}(x)-\frac{n\text J_n(x)}{x} =\frac{\text J_{n-1}(x)-\text J_{n+1}(x)}2=0\iff x\text J_{n-1}(x)=n\text J_n(x)\iff \text J_{n-1}(x)=\text J_{n+1}(x)\implies x=\text j’_{v,m}$$
where there appears the Bessel J function. Set $v=\frac12$:
$$\text J’_\frac12(x)=\frac{2x\cos(x)-\sin(x)}{\sqrt{2\pi}x^\frac32}=0\iff 2x\cos(x)=\sin(x)\iff \boxed{\tan(x)=2x\implies x=\text j’_{\frac12,m\in\Bbb N}}$$
where $m$ is the $m$th zero. This function is implemented in the DLMF, from the National Institute of Standards and Technology, so it may be a standard function. Please correct me and give me feedback.
Series solution
All solutions, except the $-1$st and $0$th solution $x=\pm 1.164\dots$, are:
$$\boxed{\tan(x)=2x\implies x_k= \left(k+\frac12\right)\pi-\sum_{m=1}^\infty\sum_{n=0}^m\frac{S_m^{(n)}\Gamma(n+m-1)(-1)^ni^{m+n}2^{m-1}}{\left((2k+1)\pi-i\right)^{n+m-1} m!\Gamma(m)}}$$
where $S_n^{(m)}$ is Stirling S1. Compare the first and second series to the actual roots. The series is from:
Let $y=\frac{\pi}{2}-x$, to solve the complementary angle.
$2x=\tan(x) → \frac{1}{\pi - 2y} = \tan(y)$
$$f(y) = \tan(y) - \frac{1}{\pi - 2y}$$ $$f'(y) = \sec(y)^2 - \frac{2}{(\pi-2y)^2}$$
Newton's method: $y_{i+1} = y_i - \frac{f(y_i)}{f'(y_i)}$, we got 0.5 → 0.407975 → 0.405237 → 0.405235
$$x=\frac{\pi}{2}-y ≈ 1.16556$$
If trig. functions not allowed, interpolation work very well too.
$f(\frac{\pi}{12}) = (2 - \sqrt 3) - \frac{1}{\pi-\pi/6} ≈ -0.1140227$
$f(\frac{\pi}{8}) = (\sqrt 2 - 1) - \frac{1}{\pi-\pi/4} ≈ -0.0101996$
$f(\frac{\pi}{6}) = \frac{\sqrt 3}{3}-\frac{1}{\pi-\pi/3}≈ 0.0998854$
$f(\frac{\pi}{4}) = 1 - \frac{1}{\pi-\pi/2} ≈ 0.3633802$
$\begin{matrix} f(y) & y \cr -0.1140227 & \frac{\pi}{12} \cr -0.0101996 & \frac{\pi}{8} & 0.405559 \cr +0.0998854 & \frac{\pi}{6} & 0.401350 & 0.405169 \cr +0.3633802 & \frac{\pi}{4} & 0.386855 & 0.405048 & 0.405215 \end{matrix}$
Inverse interpolation for $f(y)=0 → y ≈ 0.405215 → x ≈ 1.16558$
This transcendental equation does not have a closed-form formula and if the goal is to plot, there is no real benefit in computing those roots.
What you can do instead, is to plot the function $\tan x$, which has a well-known shape and is periodic, and find the intersections with $y=2x$ just graphically.
In any case, the roots are close to and odd multiple of $\dfrac\pi2$.