8

We have a circle with the known radius $r$ and the circumference $2\pi r$, and we know a point $P_1$ somewhere on it's circumference. Now, we want to get the coordinates $[x_{P_2},y_{P_2}]$ of the point $P_2$. We know the arc between $P_1$ and $P_2$ as $d = \frac{2\pi r}{x}$ where $x$ is known and $\geq 1$.

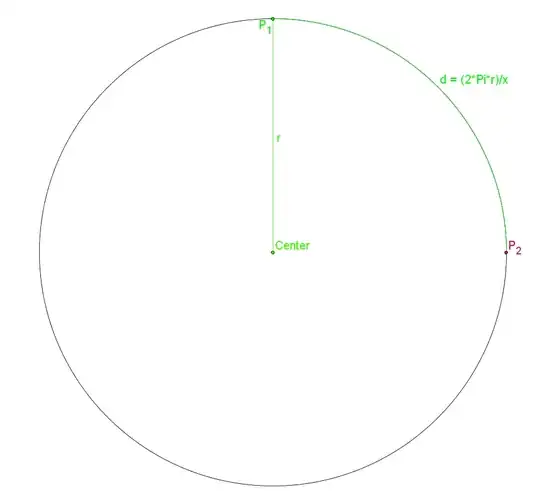
enter image description here

As a matter of fact, by knowing $d$ we know the angle from the center between $P_1$ and $P_2$, but I am unable to find a formula to get me the correct coordinates of $P_2$ for any combination of known $P_1$, $r$ and $d$.

Chris
  • 447
Big-Blue
  • 142
  • 2
  • 2
  • 9

4 Answers4

5

Let the coordinates of $P_1$ be $(x_{P_1},y_{P_1})$. Let the angle between the points $P_1$ and $P_2$ be $\theta$. Then from the arc $d$ you get, $\theta=d/r=\frac{2\pi}{x}$. So, now, we have $$x_{P_2}=x_{P_1}+r\sin{\theta};\ \\ y_{P_2}=y_{P_1}-r(1-\cos{\theta})$$.

Samrat Mukhopadhyay
  • 16,277
1

If you know $\Delta\theta$, the angle between the two points, and you know $\theta _1$, the angle of $P_1$, you can find $\theta_2$ from $\Delta\theta = \theta_1 - \theta_2$. From trigonometry, we know that $\theta_1$ is related by $y_1$ by the sine function, i.e. $\sin{\theta_1} = \frac{y_1}{r}$, where r is the radius. Thus, we can solve for $\theta_1$ and then find $\theta_2$. From there we can use the cosine function to find $x_2$ and the sine function to find $y_2$.

mangoismycat
  • 11
0

$$ x_{p2}=x_{p1} + r \cos \frac{{2 \pi}}{x}, y_{p2}=y_{p1} + r \sin \frac{{2 \pi}}{x} $$

Narasimham
  • 40,495
0

Remember, if center of circle is x = 0 and y = 0, then any point's coordinates can be found from x2 + y2 = R2 (where R is radius)

This will solve many circle questions.

pasogrande
  • 9