Wood's notation is used to reference the relationship between two 2D lattices when the angle between the two unit vectors $(a_1, a_2)$ of one lattice is the same as the angle between the unit vectors $(b_1, b_2)$ of the other lattice. It's written with the ratios of the corresponding unit vectors followed by the letter $R$ and then a rotation angle in degrees which is understood to be rounded:
$$\left(\frac{a_1}{b_1} \times \frac{a_2}{b_2}\right)R \theta $$
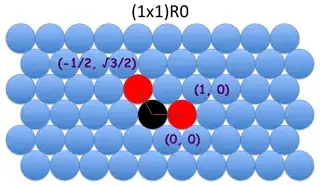
Below I show drawings of a hexagonal lattice with $a=1$ and the Wood's notation for four other commensurate hexagonal lattices.
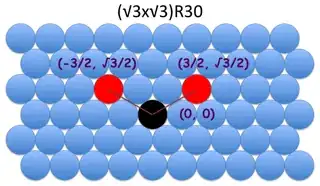
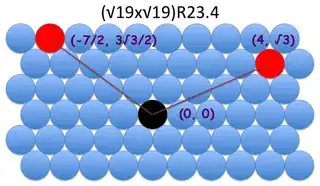
Below I show the Wood's notation and the two new vectors themselves.
Question: I've found a trivial case and three more cases of commensurate hexagonal lattices where the second lattice is enlarged by a single scalar magnification and rotated so that its lattice points match those of the unit hexagonal lattice. I've done this by trial and error. Is there a systematic way that I can find all cases (if finite) or up to some limit in size if infinite?
Ignore the trivial rotations greater than 60 degrees and less than zero, and those that are integer multiples (e.g. $\left(2\sqrt{3} \times 2\sqrt{3}\right) \text{R} 30$)
$$\left(1 \times 1\right) \text{R} 0 \ \ \ \ \left[1, 0\right], \left[-\frac{1}{2}, \frac{\sqrt{3}}{2}\right]$$
$$\left(\sqrt{3} \times \sqrt{3}\right) \text{R} 30 \ \ \ \ \left[\frac{3}{2}, \frac{\sqrt{3}}{2}\right], \left[-\frac{3}{2}, \frac{\sqrt{3}}{2}\right]$$
$$\left(\sqrt{7} \times \sqrt{7}\right) \text{R} 19.1 \ \ \ \ \left[\frac{5}{2}, \frac{\sqrt{3}}{2}\right], \left[-2, \sqrt{3}\right]$$
$$\left(\sqrt{19} \times \sqrt{19}\right) \text{R} 23.4 \ \ \ \ \left[4, \sqrt{3}\right], \left[-\frac{7}{2}, \frac{3\sqrt{3}}{2}\right]$$
Click images for full size: