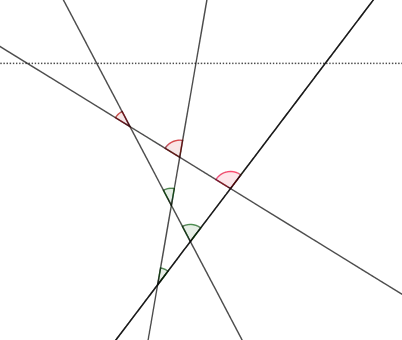2

I have $n$ lines in the plane such that no two are parallel and no three lines intersect in a common point.

Into how many finite regions do the lines divide the plane?

I came up with this recurrence relation: $$x_3=1, \qquad x_n=x_{n-1}+n-2 ,$$ and I found out it is correct. Even though I solved it intuitively, I'd like to understand how to prove this recurrence relation formally. How can I do it?

Travis Willse
  • 99,363
Raafz Morelli
  • 39
  • here is a good write up. If you search online, you'll find others. – lulu Aug 15 '19 at 16:55
  • But why do you think $X_3=1$? Three lines in general position create $7$ regions – lulu Aug 15 '19 at 16:57
  • @lulu Maybe OP wants only bounded regions. – Rushabh Mehta Aug 15 '19 at 16:58
  • 1
    @MatthewDaly and @ lulu, you seem to have missed the word "finite" in "how many finite regions." As such, both proposed links, although useful for techniques, answer the related but different question of counting how many regions are possible where we don't care if the regions are finite. – JMoravitz Aug 15 '19 at 16:58
  • @JMoravitz Ah, thank you. – lulu Aug 15 '19 at 16:58
  • NB that the proposed sequence $x_n$ is just that of the $(n - 2)$nd triangular numbers, – Travis Willse Aug 15 '19 at 17:39
  • Please include your intuitive solution. Unless it's just "good guessing", then it might well be the foundation of a formal argument, so you wouldn't want answerers to waste time (theirs or yours) telling you things you already know and/or duplicating your effort. ... Also, how do you know your recurrence is "correct"? Is it simply matching some experimental results (in which case, how far did your experiments go)? – Blue Aug 15 '19 at 18:58
  • I know it's correct because I have the recurrence relation I wrote as a solution (I'm doing a bunch of exercises about combinatorics that have solutions). The problem is that my solution is based on a mere guessing and trying case by case, maybe because of some experience with similar problems. Knowing it's not a rigourous argument, I just wanted to have a hint- or the full solution- on how I could prove it formally – Raafz Morelli Aug 15 '19 at 19:49

1 Answers1

1

We can adapt a standard trick used to solve the analogous problem for which we do not restrict to finite regions.

First, for any configuration of lines (like that of the solid lines in the diagram below), by rotating slightly we can assume that none of the lines are horizontal. Any region not bounded below has a unique lowest vertex (such regions may still be unbounded above), and conversely, every vertex is the lowest vertex of one region; in the diagram, the marked angles indicate which region is associated to each vertex.

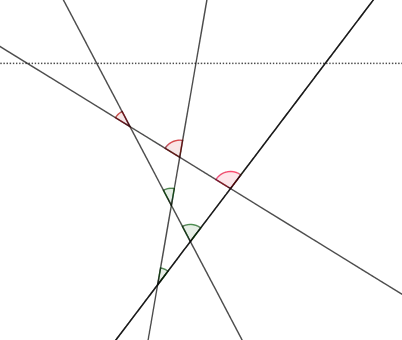
enter image description here

The number of intersections---and hence the number of regions bounded below---is at most ${n \choose 2} = \frac{1}{2} n (n - 1)$, and this number is achieved exactly when the lines are in general position (i.e., no two lines are parallel, and no three lines intersect in a point). If we draw a horizontal line above all of the intersections (like the dotted line in the diagram), it intersects all $n$ of the lines in the original configuration (again, since none of those lines are horizontal), and so there are $n - 1$ regions corresponding to a vertex and unbounded above. (In the diagram, these are the regions marked by red angles.) Since every unbounded region is unbounded above or unbounded below, the maximum number of bounded regions is $$\frac{1}{2} n (n - 1) - (n - 1) = \color{#df0000}{\boxed{\frac{1}{2} (n - 1) (n - 2) = {n - 1 \choose 2}}} .$$ A standard induction argument shows this quantity value coincides with the term $x_n$ of your sequence for every $n$.

(Alternatively, if you take as given the result that $n$ lines in general position divide the plane into ${n + 1}\choose 2$ regions (including unbounded regions), then since $n$ lines yield $2 n$ unbounded regions---to see this, draw a circle enclosing all of the intersections of the lines---there are ${{n + 1}\choose 2} - 2 n$ bounded regions.)

Travis Willse
  • 99,363