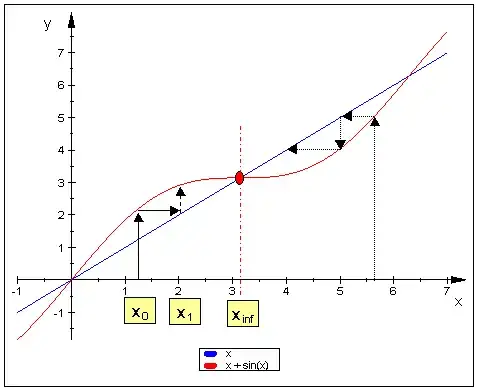
You start with $x_0 \in \mathbb R$ and define recursively for $n \ge 0$
$$x_{n+1} = x_n + \sin x_n .$$
What can we say about the convergence of the sequence $(x_n)$?
If it converges to some $x \in \mathbb R$, then necessarily
$$x = \lim x_{n+1} = \lim (x_n + \sin x_n) = \lim x_n + \lim \sin x_n = \lim x_n + \sin (\lim x_n) = x + \sin x .$$
This means $\sin x = 0$, i.e. $x = k\pi$ for some $k \in \mathbb Z$.
Case 1. $x_0 = k\pi$.
Then all $x_n = x_0$. Hence $(x_n)$ is a constant sequence which trivially converges to $k\pi$.
Case 2. $0 < x_0 < \pi$.
We claim that $(x_n)$ is strictly monotonically increasing such that all $x_n < \pi$. Hence it converges to some $x \in [x_0,\pi]$ and our above limit consideration shows $x = \pi$. The claim is easily proved by induction using the following facts:
For $0 < \xi < \pi$ we have $\sin \xi > 0$ which implies $\xi < \xi + \sin \xi$.
For $0 < \eta$ we have $\sin \eta < \eta$. For $\xi < \pi$ we therefore get $\xi + \sin \xi = \xi + \sin (\pi -\xi) < \xi + \pi - \xi = \pi$.
Case 3. $2r\pi < x_0 < (2r+1)\pi$.
Then $(x_n)$ is strictly monotonically increasing such that all $x_n < (2r+1)\pi$ and $\lim x_n = (2r+1)\pi$. This follows from Case 2 by considering the sequence $x'_n = x_n - 2r\pi$. Note that
$$x'_{n+1} = x_{n+1} - 2r\pi = x_n + \sin x_n - 2r\pi = x_n - 2r\pi + \sin (x_n - 2r\pi) = x'_n + \sin x'_n .$$
Case 4. $(2r-1)\pi < x_0 < 2r\pi$.
Then $(x_n)$ is strictly monotonically decreasing such that all $x_n > (2r-1)\pi$ and $\lim x_n = (2r-1)\pi$. This follows from Case 3 by considering the sequence $x'_n = -x_n$. Note that that $2(-r)\pi = -2r\pi < x'_0 = -x_0 < -(2r-1)\pi = (2(-r)+1)\pi$ and
$$x'_{n+1} = -x_{n+1} = -x_n - \sin x_n = -x_n +\sin(-x_n) = x'_n +\sin x'_n . $$