Why is $\sqrt{a^2+b^2}\neq a+b$, and is there another rule to simplify the square root?

Question

So I have $\sqrt{a^2+b^2}$. I thought that this was equal to $a^2+b^2$ but it is not. However, even if I convert the square root to powers, I get (based on the power rule $(a^m)^n = a^{mn}$), I get $(a^2+b^2)^{0.5} = a^1 + b^1$ but this is still not true...

Why is this, and is there any other rule for simplifying $\sqrt{a^2+b^2}$?

Answer 1

It is true that (with some restriction): $$ (a^m)^n = a^{mn}$$

It is also true that: $$ [(ab)^{m}]^n = [a^{m}.b^m]^n=[ab]^{mn}$$

You say:

$(a^2+b^2)^{0.5} = a^1 + b^1$

However This is not a general rule when you have "addition" operation raised to a power. In this specific case it is true at least when $a=b=0$

In case you have $(x+y)^m$, where $m$ is an positive integer, there is an expansion for this using the Binomial Theorem.

In case you have $(x+y)^r$, where $r$ is not an integer, there is an infinite series for this case using several approximation methods such as Taylor Expansion. There is also a binomial expansion for Fractional Exponents.

Answer 2

Actually, $\sqrt{a^2+b^2}$ is the simplest form already.

Answer 3

In power rule that you mentioned, namely $(a^m)^n=a^{mn}$, $a^m$ is a single number, whereas in $(a^2+b^2)^{0.5}$, the 0.5'th power is applied to a sum, so this is a different case.

To see that $\sqrt{a^2+b^2}=a+b$ is really false, find a counterexample. Take a=3 and b=4 for example.

Answer 4

Your first attempt amounts to

$$\sqrt s=s$$ which is obviously wrong.

Your second attempt does not fit with the power rule.

$$\sqrt{s^2}=s^{1/2\cdot2}=s$$ would be right, but is not what you considered.

---

Now have a look at

$$\sqrt{1+t^2}$$ and try to somehow relate it to $t$.

Answer 5

It is very tempting to assume that $(a+b)^{2}$ is equal to $a^{2} + b^{2}$, when, in fact, it is not.

Thus $\sqrt{a^2+b^2}$ is not equal to $a+b$. $\sqrt{a^2 + b^2}$ is about as simplified as you can go.

Answer 6

I would like to start with a principle that should be taught in all schools:

In Mathematics, Nothing Is True unless there’s a proof that it’s true.

There are a lot of formulas that look very pretty and seem very reasonable, and are true besides, like $(ab)^n=a^nb^n$, but you should have been shown in school why that formula is true.

You were undoubtedly hoping that the equally pretty and reasonable formula $(a+b)^n=a^n+b^n$ would be true, but there’s no proof for this. In fact, it’s false, but we have something much better, a formula with a stern and crystalline beauty of its own, called the Binomial Theorem: $$ (a+b)^n=a^n+na^{n-1}b + \frac{n(n-1)}2a^{n-2}b^2+\cdots+\frac{n!}{(n-j)!j!}a^{n-j}b^j+\cdots+nab^{n-1}+b^n\,, $$ valid when $n$ is a positive whole number.

The moral of my sermon? Don’t ask why an equation or formula isn’t true, because most are not true. Rather, ask what is true.

Answer 7

Answering the titular questions, which are very clear:

1. The reason that $\sqrt{a^2+b^2}\ne a +b$ is that when you square $a+b$ you don't get back $a^2+b^2$ as you should have if indeed that was the square root. In fact, you have instead $(a+b)^2=a^2+2ab+ b^2,$ which is off by the term $2ab.$

2. Well, there's no other way given all we know that we can simplify $\sqrt{a^2+b^2}$ further. It's the square root of a sum of two squares, and if $a$ and $b$ are positive it represents the length of the hypotenuse of a right triangle with legs of lengths $a$ and $b.$

Answer 8

This is a bit necro but I am surprised no one mention the distributive property¹. The reason this is not working out is because of a a misapplication of the distributive property probably due to the explanation of numaths¹.

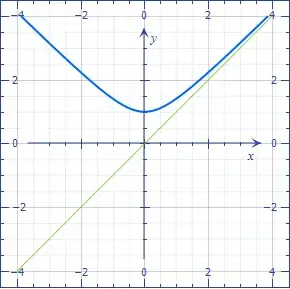
You are trying distribute exponents across addition, but exponentiation is not distributive across addition². As an aside a square root is an exponentiation to a $\frac{1}{2}$ power ($\sqrt{x} = x^\frac{1}{2}$)

You are probably used to distributing multiplicands, which is valid as multiplication is distributive across addition. In other words multiplying the sum of two or more addends produces the same result as multiplying the addends individually, and then summing the products. Using numbers:

$2(1+3) = 2 \times 1 + 2 \times 3 = 8$

$2(1 + 3) = 2(4) = 8$

Proof that exponentiation is not distributive across addition by example.

$(1+2)^2 = (3)^2 = 9 \neq 1^2 +2^2 = 1 + 4 = 5$

A more complete explanation why exponentiation is not distributive across addition can be found in this answer or by analysis in my geometric proofs.

So how does this apply to my question?

Because exponentiation is not distributive across addition one cannot distribute the exponent across the addends. This $\sqrt{a^2 + b^2} = (a^2 + b^2) ^\frac{1}{2} = a^{2 \times \frac{1}{2}} + b^{2 \times \frac{1}{2}} = a + b$, is invalid because of an illegal operation (distributing the exponent). Thus it is not possible to simplify $\sqrt{a^2 + b^2}$ more.

---

Geometric proof that multiplication is distributive across addition:

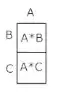[$A \times (B \times C) == A \times B + A \times C)$3" />

$A \times (B+C)$ is the same as finding the area of a rectangle with a side of length A and a side of length $B+C$, which from the picture is made up of a rectangle with sides A/B and a rectangle with sides A/C.

Geometric proof that exponentiation is not distributive across addition:

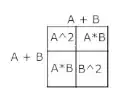[$(A+B) \times (A+B)$ does not equal $A^2 + B^2$" />

Not my best drawing but, $(A+B)^2$ is the same as finding the area of a square with a side of length A+B, from the image we see that square is made up of a Square with length A ($A^2$), square with length B ($B^2$), and two rectangles with an A side and a B side ($A \times B$).

As we can see, if we were to distribute the exponent thru the parenthesis we would miss out on rectangles AB, and BA. if $A = B$ then we have removed half the area of the square created by squaring $A+B$

You can perform this experiment yourself! Get a ruler and draw out the lengths on a sheet of paper.

---

¹ not really surprised as new math which does a horrible job at explaining simple mathematical concepts.

² However it is distributive across multiplication:

$(2*3)^2 = (2^2 * 3^2) =4 \times 9 = 36$

$(2*3)^2 = (6) ^ 2 = 36$