If we take the definition of π in the form:
π is the ratio of a circle's circumference to its diameter.
There implicitly assumed that the norm is Euclidian:
\begin{equation} \|\boldsymbol{x}\|_{2} := \sqrt{x_1^2 + \cdots + x_n^2} \end{equation}
And if we take the Chebyshev norm:
\begin{equation} \|x\|_\infty=\max\{ |x_1|, \dots, |x_n| \} \end{equation}
The circle would transform into this:
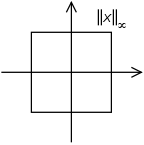
And the π would obviously change it value into $4$.
Does this lead to any changes? Maybe on other definitions of π or anything?