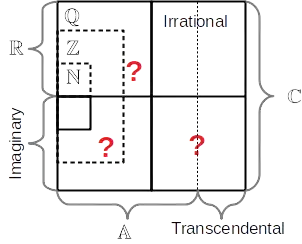
I've made a schematic of the number systems, and I noticed it's not very systematic.
Do the categories labelled with a question mark below have a name?
Specifically, imaginary integers, noninteger (real or imaginary) rationals, etc. I have not found any on Wikipedia.
Were these numbers studied in detail? E.g. imaginary number theory.