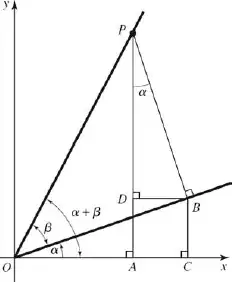
I am wondering how do these two triangles (PDB and OBC) have same alpha angle?
Asked
Active
Viewed 38 times
-2
-
1Welcome to MSE! Can you show your attempts? Or the question has a high chance to be closed. – Culver Kwan Aug 11 '19 at 12:25
-
I think you left too much to our imagination. We have to guess the construction – Lucio Tanzini Aug 11 '19 at 12:29
-
@culverkwan i was reading about why sin(a+b) is not equal sin(a)+ sin(b) in the following website https://www.oreilly.com/library/view/technical-mathematics-sixth/9780470534922/9780470534922_sum_or_difference_of_two_angles.html which i could not get how those mentioned triangles are equal. – Ehsan Jeihani Aug 11 '19 at 12:31
-
@luciotanzini this is about the proof of sin(a+b) which is available at https://www.oreilly.com/library/view/technical-mathematics-sixth/9780470534922/9780470534922_sum_or_difference_of_two_angles.html – Ehsan Jeihani Aug 11 '19 at 12:33
-
1so you don't need the two triangles to be equal, you only need the angle DPB to be equal to alpha – Lucio Tanzini Aug 11 '19 at 12:40
-
@luciotanzini good point! I edited the question. It is written that the angle between lines PD and PB is equal to the anle between OB and OC lines. Why is that? – Ehsan Jeihani Aug 11 '19 at 12:57
-
1I like my illustration of the $\sin(a+b)$ identity better. :) If you look closely, you can deduce the answer to your question from it. – Blue Aug 11 '19 at 13:02
-
1By the way ... If you want to convince yourself that $\sin(a+b)$ is generally not equal to $\sin(a)+\sin(b)$, consider $a=b=90^\circ$. – Blue Aug 11 '19 at 13:15
1 Answers
2
Assuming that $ADBC$ is a square the triangles are congruent by $ASA$
Otherwise there is not enough information to answer the question
Mohammad Riazi-Kermani
- 68,728