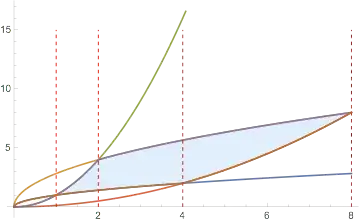
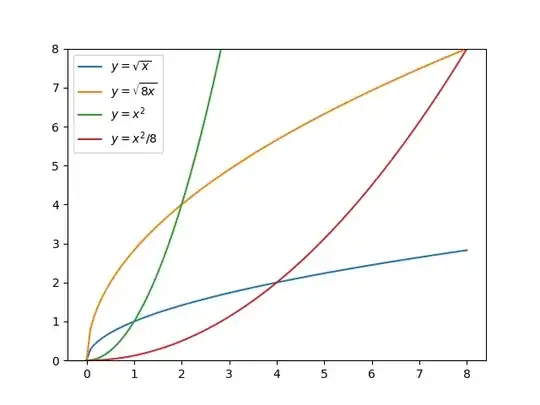
Show that the volume generated by revolving the region in the first quadrant bounded by the parabolas $y^{2} =x$, $y^{2}= 8x, x^{2}= y, x^{2}= 8y$ about the x axis is $279 \pi /2$
This problem is to be solved by changing the variables as $ y^{2} = ux , x^{2} = vy$
I can find the volume of solid of revolution when it is easy to calculate without changing variables.
Formula is given by $ \int \pi y^{2} dx$
Now how the integral will change after changing the variables$?$
$$\int\limits_{x=1}^2 \pi \left( (x^2)^2 - (\sqrt{x})^2 \right)\ dx \\ + \int\limits_{x=2}^4 \pi \left( (\sqrt{8 x})^2 - (\sqrt{x})^2 \right)\ dx \\ + \int\limits_{x=4}^8 \pi \left( (\sqrt{8 x})^2 - (x^2/8)^2 \right)\ dx \\ = \frac{279 \pi}{2} $$
Start by rewriting all the equations in terms of $y$, or even better $y^2$
$$\begin{align}y^2&=x\\y^2&=8x\\y^2&=x^4\\y^2&=x^4/64\end{align}$$
Plot the parabolas as shown below:
The intersections are at $(1,1)$, $(2,4)$, $(4,2)$, and $(8,8)$. So in terms of $x$, you have three integral domains, $1$ to $2$, $2$ to $4$, and $4$ to $8$. $$V=\pi\int_1^2(x^4-x)dx+\pi\int_2^4(8x-x)dx+\pi\int_4^8(8x-x^4/64)dx$$
