Probability of getting a sufficiently long piece from multiple stick breaking

Question

This question asks:

Start with a stick of length $1$. Repeatedly remove some fraction $U$ of the remaining stick, where $U$ is uniform in $[0,1]$. What is the probability that at least one of the removed pieces has length at least $\frac12$?

Eventually I managed to solve it, but the result was not very enlightening. Thus I present here a generalisation of the question where $\frac12$ is replaced with an arbitrary $0\le x\le1$. Let $f(x)$ be the probability that we eventually break off a stick of length at least $x$; it has been shown that for $\frac12\le x\le1$, $f(x)=-\ln x$.

What, then, is $f(x)$ for $0\le x\le\frac12$?

This generalisation is more difficult because now we can cut off more than one stick longer than $x$. Let's use joriki's approach to the source question: when $x\le\frac12$ either we cut off a piece longer than $x$ at the start, with probability $1-x$, or we leave a stick of length $t$ and replace $x$ with $x/t$: $$f(x)=1-x+\int_{1-x}^1f(x/t)\,dt$$ This is the same formula as in joriki's answer except that the lower bound $x$ has become $1-x$. We can make the same manipulations that follow there to get $$f(x)=1-x+x\int_x^{x/(1-x)}\frac{f(u)}{u^2}\,du$$ $$1-f(x)=x\left(1-\int_x^{x/(1-x)}\frac{f(u)}{u^2}\,du\right)$$ and eventually the functional differential equation $$x(1-x)^2f''(x)=f'\left(\frac x{1-x}\right)-f'(x)(1-x)^2$$ but how would I proceed from here?

I've determined the following approximate values for $f(x)$ with one million trials for each $x$.

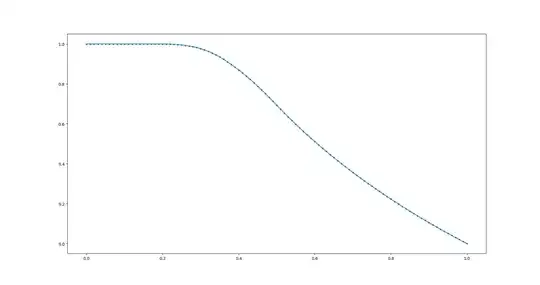
.49 .712676
.48 .732251
.47 .751341
.46 .769896
.45 .787595
.44 .805675
.43 .822355
.42 .838964
.41 .854620
.40 .869991
.39 .883803
.38 .897808
.37 .910511
.36 .923427
.35 .934614
.34 .945107
.33 .954406
.32 .963026
.31 .969796
.30 .976313
.29 .981963
.28 .986094
.27 .989759
.26 .992816
.25 .995101
.24 .996743
.23 .997929
.22 .998779
.21 .999327
.20 .999609
.19 .999815
.18 .999924
.17 .999958
.16 .999990
.15 .999995
<=.14 1.000000

Answer 1

Not an answer, but a comment (not allowed to post a comment yet) :

In the setting of random permutations on $[n]$, the law of the largest cycle is known to converge (when renormalized by $n$) to Dickman law.

I presume it will be the same here, since the same stick breaking construction applies.

The distribution of the largest fragment has distribution function $F(u)= \rho (1/u)$ where $\rho$ is the Dickman function :

$$\rho(u) =1 + \sum_{k \ge 1} \frac{(-1)^k}{k!} \int \ldots \int_{I_k(u)} \frac{dy_1 ... dy_k}{y_1 ... y_k} $$

with $$ I_k(u)=\{uy_1 >1, ..., uy_k>1, y_1+...+y_k<1 \} $$

See Arratia Barbour Tavare on page 14, formula (1.35) (Chapter 1, Permutations and primes) for the derivation.