Find all real values of the parameter $a$ for which the equation $x(x + 1)(x + a)(x + a+ 1) = a^2$ has four real roots.
My Attempt
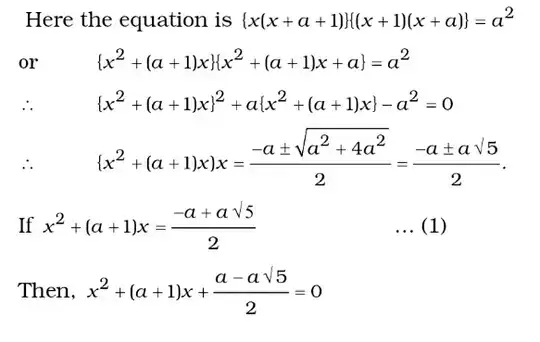



Is my attempt is correct and also is there any other way to solve this problem.
Find all real values of the parameter $a$ for which the equation $x(x + 1)(x + a)(x + a+ 1) = a^2$ has four real roots.
My Attempt
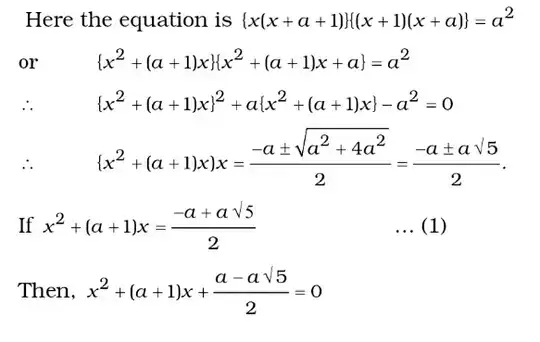



Is my attempt is correct and also is there any other way to solve this problem.
Here is a simpler solution, obtained by recognizing a certain symmetry.
Let us give names to the LHS and RHS of the given equation :
$$\underbrace{x(x+1)(x+a)(x+a+1)}_{f_a(x)}=\underbrace{a^2}_{g_a(x)} \tag{1}$$
Here are, for two cases ($a=-3$ and $a=-4.5$), the joint graphical representations of the curves of $f_a$ (blue) and $g_a$ (red). The midpoint $x_a:=-\tfrac{a+1}{2}$ of the roots of equation $f_a(x)=0$ is materialized as a little red circle.
Fig. 1 : On the left : case $a=-3$. On the right, case $a=-4.5$. In the first case, the line intersects the curve of $f_a$ only twice, meaning two real roots to equation (1) instead of four. In the second case, there are four intersection points, giving four real roots.
Whatever the value of $a$, the graphical representation of function $f_a$ will always be the same : symmetrical with respect to vertical axis with equation $x=x_a$, with a central maximum with coordinates $(x_a,f(x_a))$. The necessary and sufficient condition for having 4 roots to (1) is clearly that the ordinate of the central maximum is greater than $a^2$, i.e., $f_a(x_a)>a^2$ (see Remark 1 below). An easy calculation gives :
$$\dfrac{(a^2-1)^2}{16} > a^2$$
$$a^4-2a^2+1 > 16 a^2$$
Otherwise said :
$$(a^2-9)^2>80$$
giving :
$$a^2 \notin [9-4\sqrt{5},9+4\sqrt{5}]$$
As $9\pm 4\sqrt{5}=(2 \pm \sqrt{5})^2$, we find back your solution.
Remarks :
$$F(X):=X^4 - \tfrac12(a^2+1)X^2 + \tfrac{1}{16}(a^2-1)^2=(X^2-\tfrac{(a-1)^2}{4})(X^2-\tfrac{(a+1)^2}{4})$$
$F$ is an even "bi-quadratic" function, with variations like this
$$^{+\infty} \ \searrow \ _{_m} \ \nearrow \ ^{F(0)=M} \ \searrow \ _{_m} \ \nearrow \ ^{+\infty}$$
where $M>0$ and $m<0$.