3

$$ x^{28}+9x^{26}+39x^{24}+95x^{22}+76x^{20}-384x^{18}-1928x^{16}-4868x^{14}-7712x^{12}-6144x^{10}+4864x^{8}+24320x^{6}+39936x^{4}+36864x^{2}+16384 $$

In an example the polynomial above arose. It should have six factors, each like $$ (x^4-4x^2\cos(4\pi c_\color{blue}{\text{r}}) +4) $$ and one like $$ (x^4-4x^2\cosh(4\pi c_\color{red}{\text{n}})+4). $$ to match the degree $6\cdot4+4=28$ of the first.

Is it possible to first do the polynomial division and then determine the values of $\cos(4\pi c)$?

Or the other way: Why not just multiplying all the factors to get a set of equation? These are elementary symmetric polynomials in the variables $\cos(h)(4\pi c_{r/n})$ with integer solutions.

Is this approach known to work for a class of cases? What can we say about the angles $\cos(h)(4\pi c_{r/n})$ because of that elementary symmetric polynomial integer solution contraint?

draks ...
  • 18,449
  • The $4$th degree polynomials can further be decomposed into $\prod\big(x\pm\sqrt2\exp(\pm i2\pi c)\big)$, resp. $\prod\big(x\pm\sqrt2\exp(\pm 2\pi c)\big)$. – draks ... Sep 05 '19 at 08:08

3 Answers3

2

Let $f(x)$ be your polynomial. It has a number of symmetries. Dietrich Burde's answer exhibits one. We see another by calculating

$$g(u):=2^{-9}f(\sqrt{2u})=32 u^{14}+144 u^{13}+312 u^{12}+380 u^{11}+152 u^{10}-384 u^9-964 u^8-1217 u^7-964 u^6-384 u^5+152 u^4+380 u^3+312 u^2+144 u+32.$$

A most obvious feature of this is that it is palindromic. Meaning that $u=\xi$ is a zero of $g(u)$ if and only if $u=1/\xi$ is. A common trick taking advantage of this is to write everything in terms of the new variable $v=u+1/u$. It is simple to verify that $$ u^{-7}g(u)=P(v), $$ with $$ P(v)=32 v^7+144 v^6+88 v^5-484 v^4-960 v^3-608 v^2-84 v+23. $$ Mathematica thinks that $P(v)$ is irreducible over $\Bbb{Q}$. Judging from the plot it has five zeros in the interval $(-2,0)$ and two positive zeros approximately $0.1$ and $2.1$. If $u$ is real, then $v=u+1/u$ has absolute value $\ge2$. This would yield four real zeros of $f(x)$ subject to symmetries: $x\mapsto -x$ and $x\mapsto 2/x$.

Jyrki Lahtonen
  • 133,153
  • Have fun finding the zeros of the degree seven polynomial! – Jyrki Lahtonen Aug 08 '19 at 10:16
  • 1
    I did not double check, but factoring $P(v)$ modulo a few small primes strongly suggests that its Galois group is $S_7$. Meaning that the zeros cannot be written in terms of radicals (complex or real). More precisely, the Galois group is not a subgroup of $A_7$ and it is triply transitive. I think that's enough to conclude. – Jyrki Lahtonen Aug 08 '19 at 10:21
  • 1
    Mind you, I suspect that the origin of $f(x)$ explains the observed symmetries as well as the fact that all the zeros of $P(v)$ are real. – Jyrki Lahtonen Aug 08 '19 at 10:28
  • Jyrki, thanks a lot. The appearance of $S_7$ is sursprising, to me. The polynomial is a factor of the characteristic polynomial of the Hashimoto edge adjacency operator. The 22-vertex bicubic planar graph I've started with, doesn't look like to be connected to this group. I gotta try some more examples... – draks ... Aug 08 '19 at 10:37
  • @draks... I'm afraid I don't know how the Galois group of the extension generated by the eigenvalues of such a beast would be reflected in the structure of that graph (if at all). That is probably fun, though! Too bad I don't have the time to get into this. – Jyrki Lahtonen Aug 08 '19 at 10:41
  • 1
    gp pari ? f = 32 * x^7 + 144 * x^6 + 88 * x^5 - 484 * x^4 - 960 * x^3 - 608 * x^2 - 84 * x + 23 /// %1 = 32x^7 + 144x^6 + 88x^5 - 484x^4 - 960x^3 - 608x^2 - 84*x + 23 ? factor(f) %2 = ....irreducible.... ///

    ? polgalois(f) %3 = [5040, -1, 1, "S7"] /// ? ? polroots(f) %4 = [-1.967499859887757123187509648, -1.894434553876928033358117643, -1.157069274627468948925830743, -1.145188439085367649304516343, -0.5444281630827310208468837040, 0.1285047506388079815948074734, 2.080115539921444794028050607] ///

     – Will Jagy Aug 08 '19 at 19:23
  • Since the polynomial is a characteristic one of a matrix $W_1$ (Hashimoto edge operator; see linked question) and $\xi$ and $1/\xi$ are roots, wouldn't this point to $W_1$ being symplectic? – draks ... Sep 05 '19 at 12:36
  • 1
    @draks The $\xi\leftrightarrow1/\xi$ symmetry came only after scaling by $\sqrt2$. The zeros of the original degree 28 polynomial form orbits of the group of four transformations generated by $x\mapsto 2/x$ and $x\mapsto -x$. Those quartets are the zeros of the quartic factors $x^4-4x^2\cos(h)\alpha_i+4$. – Jyrki Lahtonen Sep 06 '19 at 21:00
  • But despite the scaling, this means that $\pm\xi$ and $\pm1/\xi=\pm\xi^\ast$ are roots and there are symplectic matrices with the same characteristic polynomial, right? – draks ... Sep 09 '19 at 15:00
1

The polynomial has two irreducible factors over $\Bbb Q$, namely $f=pq$ with $$ p=x^{14} + 3x^{13} + 9x^{12} + 21x^{11} + 42x^{10} + 78x^{9} + 124x^{8} + 190x^{7} + 248x^{6} + 312x^{5} + 336x^{4} + 336x^{3} + 288x^{2} + 192x + 128, $$

and

$$ q= x^{14} - 3x^{13} + 9x^{12} - 21x^{11} + 42x^{10} - 78x^9 + 124x^8 - 190x^7 + 248x^6 - 312x^5 + 336x^4 - 336x^3 + 288x ^2 - 192x + 128. $$

Note that the sign alternates for $q$. Now it is a bit easier to come to the six factors you want.

Dietrich Burde
  • 130,978
1

Let $P_{28}(x)$ is the issue polynomial and $$R(x) = x^{-14}P_{28}(x).$$

Then $$C(t) = R(e^{it}\sqrt2) = 4(64\cos14t+288\cos12t+624\cos10t$$ $$+760\cos8t+304\cos6t-768\cos4t-1928\cos2t-1217),$$ and $$P_7(y) = C\left(\dfrac12\arccos\dfrac y4\right) = y^7+9y^6+11y^5-121y^4-480y^3-608y^2-168y+92.$$

Another way is using of the Chebyshev Polynomials of the First Kind, then $$P_7(y) = 4(64T_7\left(\dfrac y4\right) + 288T_6\left(\dfrac y4\right) + 624T_5\left(\dfrac y4\right) + 760T_4\left(\dfrac y4\right)$$ $$ + 304T_3\left(\dfrac y4\right) - 768T_2\left(\dfrac y4\right) - 1928 \dfrac y4 - 1217),$$ with the same result (idea of OP author, see the comments).

Easily to show that $P_7(y)$ has only one root out of the interval $(-4,4)$ (proposition of the OP author, see the comments).

Since $$P'_7(t+4) = 7t^6 + 222t^5 + 2815t^4 + 17996t^3 + 59472t^2 + 90240t + 39000$$ and $$P_7(4) = -29968 <0,$$ then $P_7(y)$ has a single root on the interval $(4,\infty).$

On the other hand, $$P'_7(-4-t) = 7 t^6 + 114 t^5 + 655 t^4 + 1684 t^3 + 1968 t^2 + 896 t + 88$$ and $$P_7(-4) = 16 >0,$$ so there are not roots in the interval $(-\infty,-4).$

At the same time, the plot of $P_7(7)$

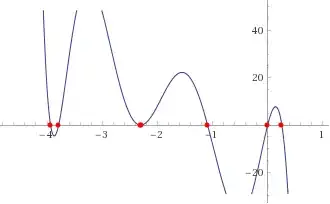
enter image description here

shows that there are six different roots in the interval $(-4,1),$ which can be easily separated.

Approximately, the roots are $$y_k\in\{4.16023,0.25701,-1.08886,-2.29038,-2.31414,-3.78887,-3.93500\}.\tag1$$

Since $$y=4\cos2t,\quad t = -i\ln\dfrac x{\sqrt2},$$ then $$y=4\cos\left(-2i\ln\dfrac x{\sqrt2}\right) = 2\left(e^{\large2\ln\frac x{\sqrt2}} + e^{-\large2\ln\frac x{\sqrt2}}\right) = x^2 + \dfrac4{x^2},$$ $$y-y_k = x^2-4\dfrac {y_k}4 + \dfrac4{x^2},$$ $$P_{28}(x) = \prod\limits_{k=0}^6\left(x^4-4\dfrac{y_k}4 x^2+4\right),\tag2$$

wherein $$y_0 > 4,\quad |y_{1-6}| <4.$$ Therefore, required decomposition of $P_{28}(x)$ is confirmed.

Yuri Negometyanov
  • 28,026
  • 1
    +1 thanks, doesn't look like there is anything special about the numerical roots. Funny that these (algebraic?) numbers end up in integers, don't you think? – draks ... Sep 09 '19 at 08:40
  • 1
    Further it is interersting that you substitute a $\cos(nt)$ with $t=\frac12\arccos(y/4)$. Isn't that related to Chebyshev Polynomials of the First Kind? That's funny, because in the history of the problem Chebyshev Polynomials of the Second Kind popped up once... – draks ... Sep 09 '19 at 08:42
  • @draks...Thank you for the comments. Both your ideas are interesting. I will correct the answer. – Yuri Negometyanov Sep 09 '19 at 10:32
  • @draks...Updated. – Yuri Negometyanov Sep 09 '19 at 12:56
  • Thanks a again. I'm not sure, about the rational coefficients part. What I meant was something like this: Geometry of Elementary Symmetric Polynomials: We have a finite product of factors $(x^4-4x^2\cos(4\pi c_{r/n}) +4)$. $\cos(...)$ might not be rational, but in the expanded polynomial, only integer coefficients show up. Doesn't this put any conditions on the angles $4\pi c_{r/n}$ to make this happen? – draks ... Sep 09 '19 at 15:09
  • @draks...We know that: 1) any integer root is the divider of 92; 2) other rational roots does not exist; 3) should work Vieta's theorem. We can be sure tthat the coefficiets are not rational. – Yuri Negometyanov Sep 09 '19 at 15:34
  • 1
    by construction the roots are given by $\big(x\pm\sqrt2\exp(\pm i2\pi c)\big)$, by that (most probably) not rational. But I'm mean the values of $c$. But maybe I just ran into something, that is not more than an idea without value...thanks again! – draks ... Sep 09 '19 at 17:49