Cauchy Schwarz: Proving this inequality

Question

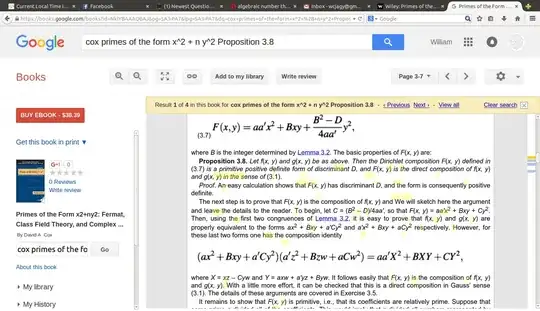
For positive reals a,b,x and y, prove that $(5a^2 + 2ab + 3b^2)(5x^2 + 2xy + 3y^2) \ge (5ax + ay + bx + 3by)^2$

My attempt: By Cauchy we can show that the LHS $\ge(5ax + 2(abxy)^{1/2} + 3by)^2$

I can then show that $ay + bx \ge 2(abxy)^{1/2}$ using AM-GM, but this doesn't help.

How can I proceed? Thank you.

It is from a post in Brilliant app, I couldn't find a way to share the link. The link is provided in a solution to the question https://brilliant.org/problems/most-awaited-question — Ram Keswani, Aug 06 '19 at 15:06

score 2 · Accepted Answer · answered Aug 06 '19 at 14:54

2

By C-S we obtain: $$(5a^2+2ab+3b^2)(5x^2+2xy+3y^2)=\left(\frac{1}{5}(5a+b)^2+\frac{14}{5}b^2\right)\left(\frac{1}{5}(5x+y)^2+\frac{14}{5}y^2\right)\geq$$ $$\geq\left(\frac{1}{5}(5a+b)(5x+y)+\frac{14}{5}by\right)^2=(5ax+ay+bx+3by)^2.$$

answered Aug 06 '19 at 14:54

Michael Rozenberg

194,933

the product is exactly $ \left( ; 5ax+ay+bx+3by ; \right)^{ ; 2} + 14 (ay-bx)^2 ,$ this being an example of Gauss composition. This (MSE) website has convinced me that students would do well to study (integer) binary quadratic forms a little before algebraic number theory; two modern, inexpensive books are Lehman https://bookstore.ams.org/dol-52/ and Weissman https://bookstore.ams.org/mbk-105/ Weissman paid special attention to possible self study – Will Jagy Aug 07 '19 at 00:15

score 1 · Answer 2 · answered Aug 06 '19 at 14:45

1

Expanding all, collecting linke terms,and factorization gives: $$(ay-bx)^2\geq 0$$ which is true.

answered Aug 06 '19 at 14:45

Dr. Sonnhard Graubner

95,283

score 0 · Answer 3 · answered Aug 06 '19 at 19:09

0

By Gauss composition, see Dirichlet's description on page 49 of the second edition of David A. Cox, Primes of the Form $x^2 + n y^2$

your product equals $$ \left( \; 5ax+ay+bx+3by \; \right)^{ \; 2} + 14 (ay-bx)^2 $$

answered Aug 06 '19 at 19:09

Will Jagy

139,541

Cauchy Schwarz: Proving this inequality

3 Answers3