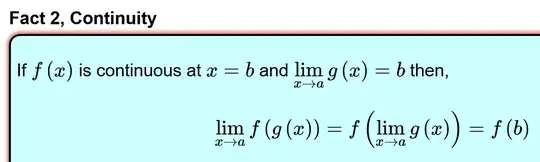Limit of composite function at isolated points

Question

Paul's Online Notes (link) writes:

I have some doubts about the above claim. In particular, I'm not sure if it's correct if $b$ is an isolated point of the domain of $f$.

I have tried to come up with the counterexample below. Is my counterexample mistaken? And if it isn't, how can we fix the above claim so that it becomes correct?

---

Counterexample. Define $f:\left\{ 2\right\} \rightarrow\mathbb{R}$ by $f\left(2\right)=3$.

Define $g:\mathbb{R}\rightarrow\mathbb{R}$ by $g\left(x\right)=x+1$

Then

• $\lim_{x\rightarrow1}g\left(x\right)=2$
• $f\left(x\right)$ is continuous at $2$ (because $2$ is an isolated point of the domain of $f$)
• $f\left(\lim_{x\rightarrow1}g\left(x\right)\right)=f\left(2\right)=3$.

However, $\lim_{x\rightarrow1}f\left(g\left(x\right)\right)$ does not exist. (The composite function $f\circ g$ is not defined for any $x\neq 1$.)

And so, contrary to the above claim, $$\lim_{x\rightarrow1}f\left(g\left(x\right)\right)\neq f\left(\lim_{x\rightarrow1}g\left(x\right)\right).$$

---

In response to Hyperion and Rick's comments, here is a screenshot from Abbott (2015, p. 122, Understanding Analysis). See especially the highlighted paragraph:

Answer 1

The definition of limit does not make sense in isolated points because in that case any real number would be the limit of the function at that point.

Recall the definition of limit:

Let $f: A \longrightarrow \mathbb{R}$ be a real function and $a$ be an adherent point of A. We say $f$ has limit $\lambda$ as $x$ approaches $a$ if for every real $\varepsilon >0$ there exists a real $\delta >0$ such that the implication

$$x\in A \wedge 0<|x-a|<\delta \implies |f(x)-\lambda|<\varepsilon$$

is true.

We can observe in the first place that as $0<|x-a|<\delta$ we don't care about the point $a$ itself so the function may not be even defined at a point and the limit can exist. For example, if we define $f:\mathbb{R}\setminus \{0\} \longrightarrow \mathbb{R}$ as $f(x)=x\sin\left( 1/x\right)$ we can see that its limit as $x$ approaches $0$ is in fact $0$.

The problem with isolated points is that if $a$ is an isolated point of $A$, then there exists a $\delta >0$ such that the set $E=\{x \in A: 0<|x-a|<\delta\}$ is empty, so given any $\lambda \in \mathbb{R}$, for every $\varepsilon >0$ the implication

$$x \in E \implies |f(x)-\lambda|<\varepsilon$$

is trivially true because $x \in E$ is always false as $E$ is the empty set, so $\lambda$ would be a limit of $f$ as $x$ approaches $a$ for every real value of $\lambda$.

So, in the situation of isolated points, the limit is not unique and so the definition would not be any useful and that is why it is required that $a$ is an adherent point of $A$.

Now we have the proper definition in detail, the theorem you posted would be:

Let $A$ and $B$ two subsets of real numbers, $a$ an adherent point of $A$ and $f: A \longrightarrow B$, $g: B \longrightarrow \mathbb{R}$ two functions that verify:

1. $\displaystyle{\lim_{x \to a} f(x)=\lambda}$

2. It is true one of the following:

   a) $\lambda \in B$ and $g$ is continuous in $\lambda$, let $\alpha=g(\lambda)$

   b) $f(x) \not = \lambda$ for every $x$ in a puntured neighbourhood of $a$ and $\displaystyle{\lim_{y \to \lambda} g(y)=\alpha}$

Then, the limit of the composed function $g \circ f: A \longrightarrow \mathbb{R}$ exits and we have

$$\alpha=\displaystyle{\lim_{x \to a} (g \circ f)(x)}=\displaystyle{\lim_{x \to a} g(f(x))}$$

To prove it, we will use the characterization of limits by sequences, so given $x_n$ any sequence convergent to $a$ such that $x_n \in A$, $x_n \not = a$ for every $n$ big enough, we must prove that $g(f(x_n))$ converges to $\alpha$.

In the first place, because of 1 we know that $f(x_n)$ converges to $\lambda$.

Now, if 2a) is true, we have that because of the continuity of $g$ at $\lambda$, $g(f(x_n))$ converges to $g(\lambda)=\alpha$.

If 2b) is true, as $x_n$ converges to $a$ and $x_n \not =a$ for $n$ big, we have that for $n$ big enough, $x_n$ would be in the puntured neibourhood given by 2b), so $f(x_n) \not = \lambda$ for $n$ big, and by the characterization of limits by sequences applied to $g$, $g(f(x_n))$ converges to $\alpha$.