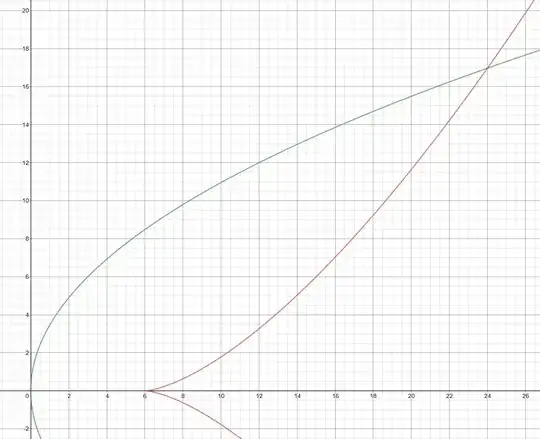
First you shall determine the domain of definition of each curve.
For the first we have
$$
0 \le y^{\,2} = {{4\left( {x - 2a} \right)^{\,3} } \over {27a}}\quad \Rightarrow \quad \left\{ {\matrix{
{x < 2a} & {a < 0} \cr
{2a < x} & {0 < a} \cr
} } \right.
$$
and for the second
$$
x = {{y^{\,2} } \over {4a}}\quad \Rightarrow \quad \left\{ {\matrix{
{x < 0} & {a < 0} \cr
{0 < x} & {0 < a} \cr
} } \right.
$$
So if $a$ changes sign, we just have a reflection around the $y$ axis, We can consider only the case $0 < a$.
Then let's determine when the first curve is over the second ($y_2 \le y_1$).
Since we have
$$
\left\{ \matrix{
27ay^{\,2} = 4\left( {x - 2a} \right)^{\,3} \hfill \cr
y^{\,2} = 4ax \hfill \cr} \right.\quad \Leftrightarrow \quad \left\{ \matrix{
27ay^{\,2} = 4\left( {x - 2a} \right)^{\,3} \hfill \cr
27ay^{\,2} = 108a^{\,2} x \hfill \cr} \right.
$$
that means
$$
\eqalign{
& 0 \le \left( {x - 2a} \right)^{\,3} - 27a^{\,2} x = \cr
& = \left( {x - 2a} \right)^{\,3} - 27a^{\,2} \left( {x - 2a} \right) - 54a^{\,3} = \cr
& = \left( {x/a - 2} \right)^{\,3} - 27\left( {x/a - 2} \right) - 54 = \cr
& = \left( {x/a - 8} \right)\left( {x/a + 1} \right)^{\,2} \cr}
$$
So, actually we have only the $y_2 = 2 \sqrt{ax}$ in $0 < x < 2a$, and $y_1 < y_2$ for $ 2a < x < 8a$.
After that, I think you can easily split the integral, and proceed by yourself.