5

I am aware that this question is related to this but I thought it would be useful to clarify a few things.

I am reading this book to get a quick overview of stochastic calculus. It introduces the Ito's lemma in an almost sure sense, 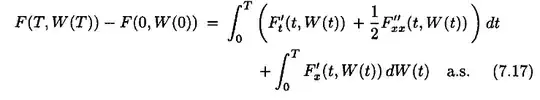enter image description here

However, the term $\int_0^T F'_x(t,W(t)) dW(t)$ is defined in the book as a limit of sums which converge in $L^2$.

In the proof of Ito's Lemma, the book always mentions that if the convergence is $L^2$, there is a subsequence that converges almost surely.

With this in mind, is it OK then to define stochastic integrals $\int_0^T f(t,W(t)) \,dW(t)$ in the almost sense? I find this confusing since this integral may not even be defined for an abritrary continuous function $f$ especially if $f$ and $W$ don't simultaneously satisfy certain variation conditions. OR, should I interpret it in this manner: Define the stochastic integral in $L^2$ and for those which converge in $L^2$, we can also define the a.s. convergence using the subsequence argument?

Hoping for clarification on the issue. Thanks!

Tomas Jorovic
  • 3,983
  • 3
  • 27
  • 38

1 Answers1

3

I'm not sure whether I understand your question correctly... so let me know if I got it all wrong.

First of all, notice that Itô's lemma is an identity of the form

$$X=Y+Z \quad \text{a.s.} \tag{1}$$

where $X$, $Y$ and $Z$ are random variables. Here, $X=F(T,W(T))-F(0,W(0))$, $Y$ corresponds to the Riemann integral and $Z$ to the stochastic integral. In order to make sense of $(1)$, it doesn't matter how the integrals are defined - it's really just that: an almost sure equality of random variables.

When proving Itô's lemma, one typically constructs sequences of random variables $(Y_n)_{n \in \mathbb{N}}$ and $(Z_n)_{n \in \mathbb{N}}$ with

  • $F(T,W(T))-F(0,W(0)) = Y_n + Z_n$
  • $Y_n \to Y$ almost surely (where $Y$ stands for the Riemann integral on the right-hand side of Itô's lemma)
  • $Z_n \to Z$ in $L^2$ (where $Z$ stands for the stocahastic integral on the right-hand side of Itô's lemma)

To conclude that $F(T,W(T))-F(0,W(0)) = Y+Z$ one chooses a subsequence $(Z_{n(k)})_{k \in \mathbb{N}}$ of $(Z_n)_{n \in \mathbb{N}}$ such that $Z_{n(k)} \to Z$ almost surely. From

$$F(T,W(T))-F(0,W(0)) = \underbrace{Y_{n(k)}}_{\to Y \, \, \text{a.s.}} + \underbrace{Z_{n(k)}}_{\to Z \, \, \text{a.s.}}$$

one now concludes that $F(T,W(T))-F(0,W(0))=Y+Z$.

Note that the existence of an almost surely convergent subsequence does not imply that we can define the stochastic integral in a pointwise sense, see e.g. this question or this question.

saz
  • 120,083
  • Hi Saz, thanks for the reply. To make the issue concrete, let's consider an application of Ito's formula where $F(t,x) = x^2$. Applied to the brownian motion, we get that

    $W(\omega,t)^2 = \int_0^t , dt + 2\int_0^t W(\omega,s) ,dW(s)$ almost surely.

    The $\omega$ above is to emphasize the sample. In other words, if I simulate a sample of Brownian motion $W(\omega,s)$ for $s \in [0,t]$, then that sample satisfies the above equality. Now for this particular sample $W(\omega,s)$, how would I compute the integral term $\int_0^t W(\omega,s) dW(\omega,s)$? This is now a deterministic quantity

     – Tomas Jorovic Aug 05 '19 at 01:23
  • Isn't the term $\int_0^t W(\omega,s) ,dW(\omega,s)$ undefined for a specific sample $W(\omega,s)$ since the Brownian motion samples aren't of bounded variation? Does this clarify my question? – Tomas Jorovic Aug 05 '19 at 01:26
  • @TomasJorovic Itô's formula is just saying that $$W(\omega,t)^2= t + 2 \left( \int_0^t W_s , dW_s \right)(\omega)$$ I put the $\omega$ outside the stochastic integral because that's all what Itô's formula is saying. Mind that the stochastic integral is defined as an $L^2$-limit and therefore $$ \left( \int_0^t W_s , dW_s \right)(\omega) \neq \int_0^t W_s(\omega) , dW_s(\omega)$$ – saz Aug 05 '19 at 06:55
  • Hi Saz, thanks for the clarification. How then would one generate samples of $\left (\int_0^t W_s dW_s \right)$ on a computer, say? Since this is an almost sure definition, then we cannot use the $L^2$ limit. It seems to me that the only way to do this would be to generate samples of $(W(\omega,t)^2 - t)/2$. Correct? In a sense, is this the purpose of Ito's formula? – Tomas Jorovic Aug 05 '19 at 20:30
  • One can use Riemann sums to approximate $\int_0^T W_s,dW_s$. If you use equally spaced partitions, the $n$th of which has spacing $2^{-n}$, and evaluate $W_s$ at left endpoints when forming those sums, then the Riemann sums converge in $L^2$ and rapidly enough that the convergence even holds almost surely, by Borel-Cantelli. The same approach (Riemann sums) would work for more general integrands under suitable conditions. – John Dawkins Aug 05 '19 at 23:04