Is the derivative of the function bounded?

Question

If a function has an oblique or horizontal asymptote but doesn't have any vertical asymptote, then can we say that the derivative of the function is bounded?

This question came in my mind while I was studying real analysis, geometrically I am able to see that it might happen but am not able to give any analytical proof.

Answer 1

Even if you restrict yourself to the case: "If a function has an horizontal or slant asymptote at $+\infty$ (or $-\infty$), there is a neighborhood of $+\infty$ (or $-\infty$) where the derivative is bounded", the statement is false.

Consider the function

$$f(x) = \frac{\sin x^3}x$$

(horizontal asymptote), or

$$f(x) = \frac{\sin x^3}x + x$$

(slant asymptote).

As an exercise you can show that, in the latter case, $$|f'(x)| > 3|x|,$$ when $x = \sqrt[3]{k\pi}$, $k\in \Bbb Z - \{0\}$.

---

EDIT Thanks to the discussion with Allawonder and the amazing counterexample given by user21820, I learned, that, rather counterintuitively, even differentiable functions that monotonically tend to an horizontal (or slant) asymptote, may have unbounded derivative.

Here I add nothing to what user21820 very precisely wrote in his answer and following comments (of which I thank him). I just want to add another counterexample of that kind, simpler than his, at the cost of losing infinite differentiability.

Take

$$t(x) = \begin{cases} 1-|x| & (|x|\leq 1) \\ 0 & (|x| > 1)\end{cases}$$

and define

$$g(x) = \sum_{k=1}^{+\infty} (2k-1) t\left((2k-1)k^2(x-2k+1)\right).$$

The function is sketched below.

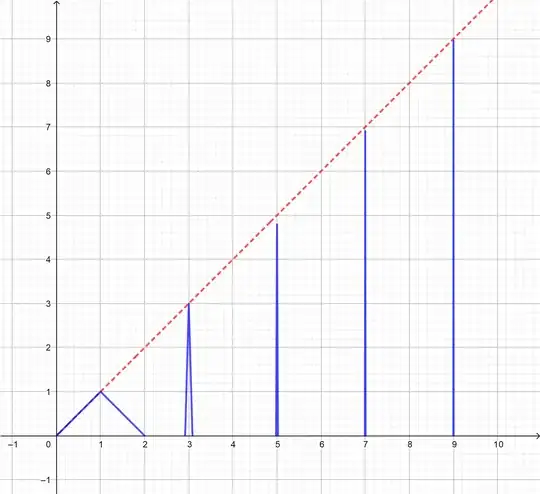
It is easy to verify that the area of the $k$th triangle is $\frac1{k^2}$.

So if we now define

$$f(x) = \int_0^{x} g(t)dt$$

we obtain a monotonically increasing function, with

$$\lim_{x\to+\infty}f(x) = \frac{\pi^2}{6}$$

with unbounded derivative.

Answer 2

No, consider the exponential function $f(x) = e^x$ defined for all real numbers. It has a horizontal asymptote (the horizontal $x$-axis) but has no vertical asymptote (by vertical asymptote I assume you mean something like $1/x^2$ at $x=0$) however, its derivative $f'=f$ is unbounded.

Answer 3

Consider the function $f$ on $(0,∞)$ defined by $f(x) = \sin(x^3)/x$ for every $x∈(0,∞)$.

It has a horizontal asymptote at $∞$, but obviously has unbounded derivative.

A natural question that arises is whether the derivative must always be bounded if the function is differentiable and monotonically approaches a non-vertical asymptote (i.e. the difference between the function and the asymptote tends monotonically to zero). The answer is still no.

Consider the function $g$ on $(0,∞)$ defined by $g(x) = \int_0^x t·(\cos(t)^2)^{t^4}\ dt$ for every $x∈(0,∞)$. (In case you cannot see, the outer exponent is $t^4$.) Note that the squaring of $\cos(t)$ is to ensure that the outer exponentiation is well-defined.

Then clearly $g$ is monotonically increasing, and I'll leave it as a fun exercise for you to prove that $g$ is bounded, and hence $g$ has a horizontal asymptote. But $g'(x) = x·(\cos(x)^2)^{x^4}$, which is clearly unbounded even as $x→∞$. Moreover, $g$ is infinitely differentiable!

Hints for the exercise:

(1) $c^{t^4} ≤ c^{(k·π)^4}$ for every $c ≥ 0$ and $t∈[k,k+1]·π$.
(2) To bound $\int_0^{π/2} (\cos(t)^2)^{p^4}\ dt$, prove that $\cos(t)^2 ≤ \exp(-t^2/2)$ for every $t∈[0,π/2]$, and so $\int_0^{π/2} (\cos(t)^2)^{p^4}\ dt ≤ \int_0^{π/2} \exp(-p^4·t^2/2)\ dt = \int_0^{π/2} \exp(-t^2/2)\ dt / p^2$.

Answer 4

Edit-Edit: From the answer of @user21820 it appears that even in the case where a function monotonically approaches an asymptote it still doesn't follow that the derivative should be bounded at infinity. This is a real lesson in the possibility of being badly misled by intuition.

---

Edit: As the counterexamples of @dfnu show, having an asymptote at infinity doesn't imply a bounded derivative near infinity, as I assumed in my previous answer below. I'm leaving this because I think you were thinking along similar lines. I wouldn't normally think of a snaky curve as being asymptotic, but it fits the definition nicely, so one has to admit that this is not true in general. It's probably true only for curves that are monotonically asymptotic to a line -- which were the only type I'd (insufficiently) had in mind while composing the previous answer below.

---

I see what might have led you into this thinking. Having a nonvertical asymptote means the derivative has a limiting value at $\pm \infty,$ but that's all that one can conclude -- without additional hypothesis.

Thus, it doesn't follow that if a function has a limiting value then it is bounded -- except for some classes of functions -- namely those defined on $(-\infty,a]$ or $[a,+\infty)$ for some real $a,$ and which are continuous at their finite endpoints, or else those defined on $(-\infty,+\infty)$ and having asymptotes at both "endpoints". That is, you've been implicitly (if my retracing of your thinking is correct) making the assumption that your function should be defined only on half-open intervals with one infinite endpoint and continuous at the finite endpoint -- or else it must have asymptotes at both $+\infty$ and $-\infty.$ These are additional conditions that guarantee that the derivative is bounded.

So, for example, you might originally have been thinking of something like the arctangent function defined on the real line. Thus, if a function is defined and continuously differentiable on $\mathbf R,$ and it has asymptotes at both $+\infty$ and $-\infty,$ then it's derivative should be bounded. If it's defined and continuously differentiable on either $(-\infty,a]$ or $[a,+\infty),$ and it has an asymptote at $\pm \infty,$ then again the derivative is bounded. An example of such would be the exponential function defined for $x\ge 0.$

I think this was what you had in mind. Now that we have clarified the problem can you try to find a proof?