0

Prove that for $c,r>0$,

if $\langle a,b\rangle\cdot\langle p,q\rangle=ap+bq>0$ then the bisector of the obtuse angle is $\dfrac{ax+by+c}{\sqrt{a^2+b^2}}=\dfrac{px+qy+r}{\sqrt{p^2+q^2}}$

if $\langle a,b\rangle\cdot\langle p,q\rangle=ap+bq<0$ then the bisector of the acute angle is $\dfrac{ax+by+c}{\sqrt{a^2+b^2}}=-\dfrac{px+qy+r}{\sqrt{p^2+q^2}}$

What I knw

$<a,b>$ is one of the vector perpendicular to the line $ax+by+c=0$ and $<p,q>$ is one vector perpendicular to the line $px+qy+r=0$.

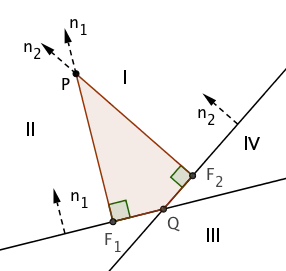
If the signed distance is positive, the normal vector points from the line towards the point, while a negative value means that the normal points away from the point. The two intersecting lines divide the 2d plane into four halfplanes say $L^+_1,L^+_2,L_1^-,L^-_2$ depending on the sign of $ax+by+c$ and $px+qy+r$. One of the angle bisectors will go through the regions $L_1^+,L_2^+$ and $L_1^-,L_2^-$, in which both the normals are either pointing away or towards the points. Thus we can draw the quadrilateral as shown by @amd.

enter image description here

And, if the angle between normals is acute, ie. $n_1.n_2=-n_1.-n_2> 0 $ then the angle between line and bisector is obtuse. ie. the obtuse angle bisector is $\dfrac{ax+by+c}{\sqrt{a^2+b^2}}=\dfrac{px+qy+r}{\sqrt{p^2+q^2}}$.

if the angle between normals is obtuse, ie. $n_1.n_2=-n_1.-n_2< 0 $ then the angle between line and bisector is acute. ie. the acute angle bisector is $\dfrac{ax+by+c}{\sqrt{a^2+b^2}}=-\dfrac{px+qy+r}{\sqrt{p^2+q^2}}$.

This is clear !!! Except,

Doubt

I think in order to find the obtuse and acute angle bisector we need to choose the normals of the lines both pointing either towards the point or away from the point. And may be that is where the condition $c,r>0$ or $c,r<0$ comes in. It'd be helpful if someone could clarify this ?

Note

I have gone through a similar post,answer by @amd, How do I prove this method of determining the sign for acute or obtuse angle bisector in the angle bisector formula works?, which tries to prove this condition but the part that involves my doubt is confusing for me.

Community
  • 1
Sooraj S
  • 7,573
  • The question, as written, is almost meaningless. Perhaps you meant to say that the vectors $(a, b)$ and $(p, q)$ form an obtuse angle at the origin, but that, of course, is false, as you can see by taking $(a, b) = (1,0)$ and $(p, q) = (1,1)$. The appearance of the letter $c$ in the second part of the question also suggests that you've messed up in using "q" twice on the right-hand side, and it should be replaced by "r" for symmetry. Of course, neither has any meaning elsewhere, so it's a little baffling. Could you (a) draw a picture, and (b) clearly describe what you're trying to prove? – John Hughes Aug 02 '19 at 17:39
  • Flipping the normal vectors produces a similar picture, but with the four regions relabeled. There’s nothing in the proof that depends on the particular choice of orientation, nor does it depends on a lucky guess that has both normals pointing into the obtuse angle, as I arbitrarily chose to depict. The four regions are identified by the combinations of signs of the signed distances to the two lines, which are determined by the two normals, which are ultimately taken directly from the two given equations. There’s no “choice” involved. – amd Aug 03 '19 at 00:24
  • @amd i think may b i'm confused with how the signed distances determine the direction of the normals ? ..how do I show that?..And there is also a condition that $c, r>0$ before taking the dot product between the normals ? ..could u pls explain bit more on that part ?. – Sooraj S Aug 03 '19 at 13:24
  • @JohnHughes I have edited my post. please check if i explain my doubt clearly – Sooraj S Aug 03 '19 at 14:21
  • @amd i have also updated my doubt, hope its now better explained – Sooraj S Aug 03 '19 at 14:21
  • The highlighted box makes no sense; everything in it is undefined. The next sentence talks about "the given lines," but no lines have been mentioned. Here's how your question might begin, in a reasonable rephrasing: "Suppose $a^2 + b^2 \ne 0$ and $p^2 + q^2 \ne 0$; then we have halfplanes defined by $ax + by + c \ge 0$ and $px + qy + r \ge 0$, with their boundary lines being defined by $ax + by + c = 0$ and $px + qy + r = 0$, and the intersection of the halfplanes is a region $R$ bounded by parts of the lines, with some enclosed angle $\theta$ \ldots" See how that's different and clearer? – John Hughes Aug 03 '19 at 16:04
  • I see you're new to MSE. Here's a general tip: make your question easy to read for the people who will be answering -- they are, after all, helping you, so maybe you should help them. That includes using complete sentences, avoiding cryptic shorthand ("+ive"?) and checking spelling ("bi heart"?). It also helps to do your very best to say exactly what your question is. In this case, it appears that it might be, "Why, when this dot product is negative, must that angle be obtuse?", although it'd help if you'd make really clear what "this" and "that" mean in this question. – John Hughes Aug 03 '19 at 16:27
  • Also: read that first sentence in the box. The word "if" is missing. Not a good sign that you respect the time of those reading your question. – John Hughes Aug 03 '19 at 17:29
  • @JohnHughes thanks for your remarks and correction, I really appreciate it as it'd be helpful for people like me who are quite new to this site and depending on stackexchange forum for learning math. I have tried to correct OP as per your suggestions, and it'd be very helpful if u could help me clarify my doubts. – Sooraj S Aug 03 '19 at 22:36
  • @amd the four regions are determined by the signed distances, i understand that. But, I do not understand how the signed distances depends on the normals that we take when the constant term$(c,r>0)$ in the equation of the line is positive. – Sooraj S Aug 04 '19 at 06:52
  • So you thank me for my remarks, but leave your question as it stood, adding at the very end another sentence with another mis-spelling. Sigh. Here's the truth: I can pretty much guess the question you're trying to ask, and I can certainly answer it ... but I'm not going to. Because I suspect it'll turn out that I've guessed a tiny bit wrong, and then you'll correct the question and add another one, and I'll be headed down a rathole. Please, please, show some actual effort at clarity. Sigh. Call me Sisyphus... – John Hughes Aug 04 '19 at 14:15
  • @JohnHughes I have again edited the post, tried my best to explain where my doubt lies in. I have been sitting on this problem for days to understand this completely. And, "English" is not my native language, hope people here could ignore few mistakes in it, though I tried to rectify them. And I am relying on stackexchange forum to learn math myself so I fully understand the importance of any comments and suggestions people add here taking their precious time without expecting anything from me or anyone else. – Sooraj S Aug 04 '19 at 21:40

0 Answers0