Justifying the "onion proof" for circle area

Question

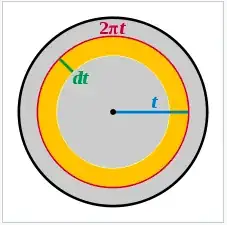
I was, as we all were, exposed to the so-called "onion proof" in my first calculus course in high school. Courtesy of this shameless screengrab from wikipedia, the proof can be visualized by integrating across infinitely many, infinitely thin rings which can be approximated by rectangles of length $\ 2πt$ and width$\ dt$.

Now, how can we justify the approximation of the area bounded by the two circular arcs as a rectangle? Is it possible to show unequivocally that:

$\ 2π(t-dt) \times dt$ < area of ring < $\ 2πt \times dt$

for instance, and then apply squeeze theorem as$\ dt$ goes to zero in the limit? I am aware that this approximation is connected to deeper facts about the Jacobian of a polar transformation, but I would like to prove the above inequality with as little machinery as possible (in order to avoid potential circularities in my logic...) If it is not possible to do so rigorously, this feedback would also be appreciated.

@NickD. Perhaps I misunderstand, but wasn't the OP in fact trying to derive the area formula for a circle? — rogerl, Jul 31 '19 at 22:21
D'oh. Thanks, @rogerl. Will remind myself to actually read questions carefully. — Nick D., Jul 31 '19 at 22:36
I think that you might be focused on the wrong aspect of the approximation. What matters for the integral isn’t how closely an individual “infinitesimal” annulus is approximated by the “infinitesimal” rectangle, but whether or not the total error made by adding up these approximations vanishes in the right way as the size of the mesh goes to zero. — amd, Aug 01 '19 at 23:41
Well, in order to establish that the integrand we write is valid, I believe we are forced to make the appeal that the area of an annulus can be approximated arbitrarily well by a rectangle of area 2πt×dt, for small enough dt. Every time I have seen or been shown this proof, a geometric appeal has always been used to justify this initial logical leap. I'm not suggesting that "infinitesimals are real", if that's what you're worried about :) — Math Enthusiast, Aug 02 '19 at 01:39
Not really. My concern is that even if one somehow shows that the individual approximations to each “slice” are good, the slices themselves might not be appropriate (viz common student errors in computing areas of surfaces of revolution, for instance). If you want to try to make these “proofs” rigorous, you really have to examine the relevant Riemann sums. All of the appeals to adding up some collection of infinitesimal slices is just a gloss over that, anyway. — amd, Aug 02 '19 at 04:55
I think I understand the gist of what you're saying, and it appears to accurately point out some fixation error on my part :) I would be interested to hear of what I'm missing in more detail — Math Enthusiast, Aug 02 '19 at 13:38

score 1 · Answer 1 · answered Jul 31 '19 at 22:27

1

This is a justification for the use of the rectangle but it might not be quite as rigorous as you're hoping for.

The arc length of the circle at a given radius, $r$, is double the arc length of $\sqrt{r^2-x^2}$, which represents the semicircle of radius $r$. We can use the formula for arc-length to calculate this as

$$\begin{aligned}2\int_{-r}^r\sqrt{1+\left(\frac{\mathrm{d}}{\mathrm{d}x}\sqrt{r^2-x^2}\right)^2}\ \mathrm{d}x &=2\int_{-r}^r\frac{r}{\sqrt{r^2-x^2}}\ \mathrm{d}x \\ &=2r\int_{-1}^1\frac{1}{\sqrt{1-x^2}}\ \mathrm{d}x \\ &=2\pi r \end{aligned}$$

where we define the constant expressed by the last integral as $\pi$.

So, we find the area of the ring by integrating over $r$.

$$\begin{aligned}\int_{t-\Delta t}^{t}2\pi r\ \mathrm{d}r &=\left[2\pi\frac{r^2}{2}\right]_{t-\Delta t}^{t} \\ &=\pi t^2-\pi(t-\Delta t)^2 \\ &=2\pi t\Delta t-\pi \Delta t^2 \end{aligned}$$

The term $\Delta t^2$ essentially vanishes faster than $\Delta t$. So, as $\Delta t$ approaches $0$, the area is well approximated by $2\pi t\Delta t$. I.e. a rectangle of side lengths $2\pi t$ and $\Delta t$.

NB: I recycled some content in this answer from this answer of mine.

answered Jul 31 '19 at 22:27

Jam

10,325

1

My main problem is where we would write the integral from t-dt to t. The justification for that step seems to already imply that the approximation is valid – Math Enthusiast Jul 31 '19 at 22:46
@MathEnthusiast That's a very good point. I might be way off but surely it's sufficient that $2\pi r$ is linear wrt. $r$, so the area of the ring is well defined since it's the integral of a linear function? – Jam Jul 31 '19 at 22:59
Yeah, I'm tempted to invoke the intuitive idea that the circumference is the derivative of the area function and call it a day. But every time I see this proof, people always use the geometric reasoning about the rings becoming rectangular in the limit...anyways, thanks for humoring my skepticism :) – Math Enthusiast Jul 31 '19 at 23:15
@MathEnthusiast You're very welcome but it's not at all just humoring; I'm genuinely skeptical about the fact too. So, if I find a convincing argument, I'll edit this answer and get back to you. This question is very similar to yours and some comments reference the justification of multiplying the length of the ring by $\Delta r$. But it is slightly taken for granted. – Jam Jul 31 '19 at 23:24
I suppose another way of justifying it would be that, since the length of the circles is $2\pi r$ and, heuristically, the change in area between circles of radius $(r-\Delta r)$ and $r$ should correspond with the change in area under $2\pi r$ between $(r-\Delta r)$ and $r$. Then the area of the ring is equal to that of the trapezoid with width $\Delta r$ and lengths $2\pi(r-\Delta r)$ and $2\pi r$. Which again is equal to $2\pi r \Delta r - \pi \Delta r ^2$. But I think to get a fully convincing motivation for where the area comes from, you'd likely have to use more powerful tools. – Jam Jul 31 '19 at 23:43
1

A lot of people will default to the double integral technique that uses polar coordinates, which they claim is more rigorous. The problem I have with that, though, is that the factor "r" in rdrdθ drops out of the Jacobian in a process that uses the derivative of sin(θ). Now, if we prove the derivative of sin(θ) by examining the limit of sin(θ) / θ , we will have a logical circularity because proofs of this limit must rely on the formula for circle area! You can maybe escape by using the geometric proof for the derivative of sin(θ), but that's not great because it's pretty intuitionistic too. – Math Enthusiast Aug 01 '19 at 00:34
1

@MathEnthusiast How does computing the limit of $\sin x/x$ require knowing the formula for the area of a circle? A straightforward comparison of a circular sector with certain inscribed and circumscribed right triangles gives you $\sin x\le x\le\tan x$ and then you use the squeeze theorem. – amd Aug 01 '19 at 07:11
1

As discussed in the first answer to this question, the comparison of areas which yields the initial inequality requires that we know the area of a circular sector (and therefore circle) given its arc: https://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 – Math Enthusiast Aug 01 '19 at 13:05
I agree it seems circular but surely it would be solved by just using the analytic definition of $\sin$, no? – Jam Aug 01 '19 at 14:41
That might be the only way to resolve everything rigorously. Just personally, it feels like cheating to use a simple definition to prove results, and then later adopt these results as definition that would appear completely unmotivated for a person who hadn't first learned the original definition. Imagine showing a middle school student Terence Tao's book where he defines sin(θ) a priori as its complex exponential representation...haha – Math Enthusiast Aug 01 '19 at 16:14
@MathEnthusiast Sure but isn't that true about math in general? Taking something natural and formalising it. We wouldn't have groups without intuitive notions of integers, axiomatic geometry without primitive understandings of 3d space, probability without gambling, etc. – Jam Aug 01 '19 at 16:46
Philosophically, yeah :D When it comes to avoiding logical circularities though, I tend to shy away from generalization in favor of a more minutia driven approach. In the case of something as simple as the area of a circle, for instance, more complexity makes me worry that I haven't truly understood. – Math Enthusiast Aug 01 '19 at 17:02
Doesn’t this answer beg the question? Finding the area of the ring by integrating over $r$ essentially involves making the same approximation that you’re trying to justify. That aside, the observation at the end about $\Delta t^2$ is really the key—that’s going to be why the error in the Riemann sum vanishes “fast enough.” – amd Aug 06 '19 at 23:43
@amd Indeed it does beg the question. But I only realised that in the subsequent discussion in the comments. Imo your point a while ago about the overall error of the Riemann sum vanishing is the best explanation. And imo you could even illustrate the point with an example of a Riemann sum composed of some kind of 'strip' that seems counterintuitive and unjustified but still ends up with the Riemann sum's error vanishing. If you'd like to put up an answer that covers what you've put in the comments, that'd be cool; otherwise, I'll just edit my answer to try to address it better. – Jam Aug 07 '19 at 00:55
Personally, I think OP's point about sin(x)/x being circular is tangential and the main point is the one about Riemann sums. Plus the sin(x)/x confusion is fielded by other questions on the site – Jam Aug 07 '19 at 00:58

Justifying the "onion proof" for circle area

1 Answers1