What is the derivation of the trigonometric functions (90°-θ; 90°+θ)

Question

How are these reduction formulas derived?

$$\sin(90°+θ) = +\cos(θ)$$ $$\cos(90°+θ) = -\sin(θ)$$

I understand how to reduce angels that fall into the $2^{nd}$, $3^{rd}$, and $4^{th}$ quadrants to be expressed in the $1^{st}$ quadrant at $180°$ and $360°$ differences but not at $90°$.

Thanks for the help.

Welcome to Mathematics Stack Exchange. You could apply angle addition formulas — J. W. Tanner, Jul 31 '19 at 14:15
See this answer. (The current question might be considered a duplicate.) — Blue, Jul 31 '19 at 14:29
@blue ah... that answer has clear and pretty pictures. The picture the OP linked is ugly and not clear. — fleablood, Jul 31 '19 at 14:36
It’s called cosine because it’s literally the sine of the complementary angle. — gen-ℤ ready to perish, Jul 31 '19 at 15:08
@let'shaveabreakdown that is very nice to know! But it begs the question as to why if $r\sin \theta = x$ and $r=\sqrt{x^2 + y^2}$ then why does $y = r\sin (90 -\theta)$. — fleablood, Jul 31 '19 at 16:06
..... of course putting the question in terms of "if $(x,y)$ is a point of with angle $\theta$ so that $r = \sqrt {x^2 + y^2}$ and $\sin \theta := \frac xr$ then why does $y = \sin (90-\theta)$" is actually a lot harder to ask than it is to answer! — fleablood, Jul 31 '19 at 16:12

fleablood · Accepted Answer · 2019-07-31T14:40:13.683

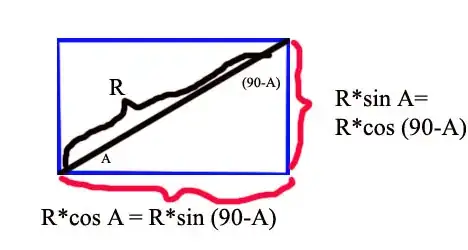
Okay....

take a point $(x,y)= (r\cos \theta, r\sin \theta)$. Rotate your plane $90$ degrees counter clockwise. The point will have moved from $(x,y)$ to $(-y, x)=(r\cos (\theta + 90), r\sin (\theta + 90))$.

So $r\cos (\theta + 90) = -y$ and $r\sin (\theta+90) = x$.

That's all.

Okay, why does $(x,y) \mapsto (-y, x)$?

Well.... draw the line from $(x_0,y_0)$ to $(0,0)$, That line has the formula $y = \frac {y_0}{x_0} x$ and slope of $m= \frac {y_0}{x_0}$. A line that is $90$ degrees from this to the origin will have a slope of $-\frac 1m = \frac {x_0}{y_0}$. If you move along the perpendicular line with the perpendicular slope the same distance of $r = ||(x_0, y_0), (0,0)|| = \sqrt {(x_0-0)^2 + (y_0-0)^2}$ you will get to the point $(-y,x)$.

Or in other words:

$(x,y)$ is the result of going to the right $x$, and going up $y$. If you rotate that $90$ degrees, you will be going up the same distance you used to go right. So you'll go up $x$. And you'll go left the same distance you used to up. So you'll go $y$ to the left--- of $-y$. So you'll end up at $(-y, x)$; which is going to the left $y$ and up $x$.

....

ANd blue posted a comment with a link to: https://math.stackexchange.com/a/737353/409

The OP posted this picture:

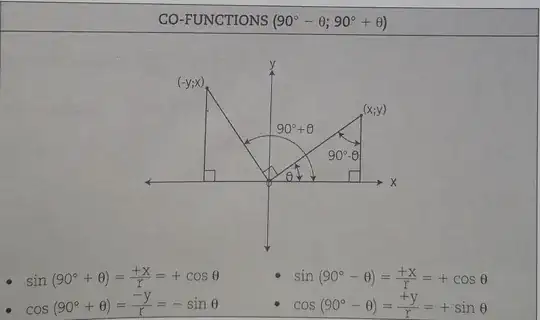
which is kind of ugly and not very clear.

But the posted answer has this picture:

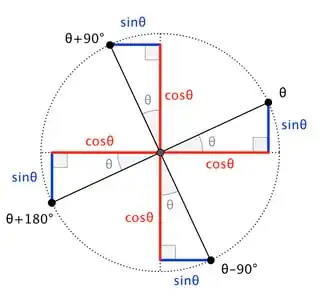
which I think is just beautiful and utterly clear.

score 0 · Answer 2 · answered Jul 31 '19 at 16:32

let's have a breakdown in the comments made a VERY interesting point that "co-sine" literally means "sin of the complimentary angle" so by definition $\cos A = \sin (90 -A)$.

The question is if $(x,y)$ is a point where $R= ||(x,y)||=\sqrt{x^2 +y^2}$ so that we have $y = R*\sin A$ (by definition of "sine") then why would it follow that $x$ should equal $r*\sin (90-A)= R*\cos A$.

Which encouraged me to create the following image which should make that clear.

If $y = R*\sin A$ then it follows that $x = R\sin (90-A)$.

We can either define $\cos A = \frac yR$ or we could define $\cos A = \sin (90-A)$. But the picture should explain why those two values are always the same.

(Absolute and sincere thanks to Let's have a breakdown for suggesting this line of thought!)

What is the derivation of the trigonometric functions (90°-θ; 90°+θ)

2 Answers2