Where the modulus-like symbol actually denotes iteration of a radical function. Sorry for the messy work everyone- I am new to this stuff, and I literally just found this iteration formula like 15 minutes ago. $X[i]$ starts as being an arbitrary number greater than $n!/(n-2)!$ which I should have mentioned earlier but didn't have space to (apologies). So the business is: you start with a number e.g. 1, then if you want to find say $50$, you compute $sqrt(1 + 50!/48!)$ then replace $1$ on your calculator with the result you just got a.k.a. $Ans$ etc. and keep iterating till you get (at a surprisingly fast convergence rate!) the very number you started with, n.
I appreciate this might not be the most interesting insight or $n!/(n-2)!$ is probably just me not realising that it could also be presented as $n(n-1) = n^2-n$. But still, please don't mass-downvote it all, remember it's a 15-year old person who figured this out...
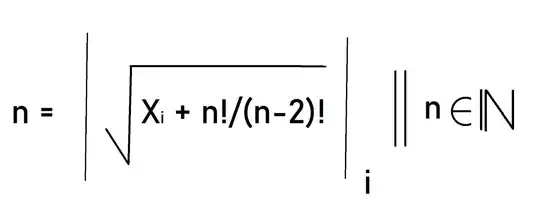 $\sin^2 \theta$">
$\sin^2 \theta$">