I was going through the following optimization problem:
 Also there was a hint with this problem as:
Also there was a hint with this problem as:
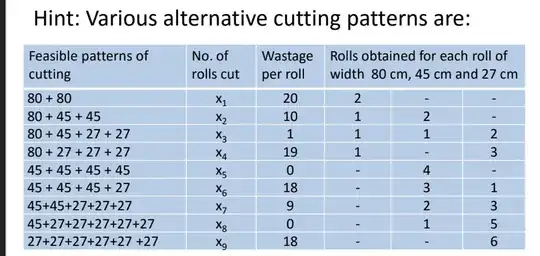
Above are listed nine alternative ways to cut the paper. Clearly the wastage per roll is always less than $27$, because if we get $30$ cm as wastage then that means that we can still get a roll of $27$ cm and so the wastage is $3$. This one thing is clear to me. Is there any method by which I can get that total number of alternatives are nine OR I have to do it manually?
What I have done:
Out of $180$ cm roll we can get $0,1$ or $2$ rolls of $80$ cm, for $45$ cm roll we have options $0,1,2,3$ or $4$ and for $27$ cm roll we have options $0,1,2,3,4,5$ or $6$. From this information maximum number of combinations would be $3\times 5 \times 7=105$. Here I was unable to use the information that the wastage will be less than $27$ cm.
Next I listed all the possibilities as triplets:
$(0,0,0),(0,0,1),(0,0,2),....,(0,0,7)$
$(0,1,0),(0,1,1),(0,1,2),....,(0,1,7)$
$....................................$
$(0,4,0),(0,4,1),(0,4,2),....,(0,4,7)$
$(1,0,0),(1,0,1),(1,0,2),....,(1,0,7)$
$....................................$
$....................................$
$(2,4,0),(2,4,1),(2,4,2),....,(2,4,7)$
So now we have $15$ rows in total. And from each row at most we have only one entry which is suitable for us. Because if in a row we have $(a,b,c)$ as a suitable entry then that means that $(a,b,c-1)$ will give a wastage of more than $27$ cm so its not good for us and $(a,b,c+1)$ is not possible because $(a,b,c)$ has wastage less than $27$ cm. So we have $15$ rows so at most we have $15$ combinations which is suitable for us.
The last $5$ rows, rows with first entry as $2$. Out of all these we have only $(2,0,0)$ suitable for us. So out of last $5$ rows we have only one entry $(2,0,0)$ which is suitable for us. So now for the first $10$ rows we have at most $10$ suitable combinations and one from the last $5$ rows. Total will be maximum $10+1=11$.