0

Im trying to wrap a wire on two nails on a flat plane. I need to calculate the angle of a length of wire with respect to the x axis, given the thickness of two nails, and their locations, and different wire thicknesses.

To do that, I believe it requires defining a wire segment as rectangle with two opposing corners tangent to two known circles as in the picture below.

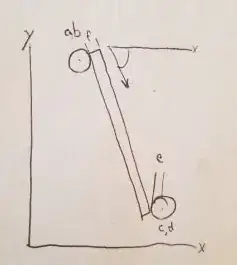
Wire touching two nails

Keith Reynolds
  • 103
  • Please draw a figure for us. – David G. Stork Jul 26 '19 at 18:32
  • Please edit your post to state which part(s) of the wire are you trying to figure out an angle, and an angle with respect to what (e.g., the positive $x$-axis). Thanks. – John Omielan Jul 26 '19 at 18:50
  • @KeithReynolds Thanks for providing more details. I believe I've figured out your answer, but I first want to confirm a few things. The $2$ circles are the nails and the rectangle is the wire. The center of the upper circle is $(a,b)$ & the lower circle is $(c,d)$. The radii of both circles is $e$. The width of the wire is $f$. Finally, I'm assuming $a \lt c$ and $b \gt d$, although the calculations don't actually depend on this. Please let me know if any of this is incorrect. Thanks. P.S. I was planning on giving an exact answer, with amd's answer, I believe, being only approximate. – John Omielan Jul 26 '19 at 19:21
  • @JohnOmielan Yet another instance of how to compute common tangents to a pair of circles adds little to this site, IMO. How to solve that part of the problem has been explained many times already. – amd Jul 26 '19 at 19:24
  • @JohnOmielan those assumptions are correct. – Keith Reynolds Jul 26 '19 at 19:24
  • @JohnOmielan It is exactly the same problem as finding the common tangent to a pair of circles, just not to the original ones given. – amd Jul 26 '19 at 19:30
  • @amd I feel a bit silly. Of course, it is with one of the circles being somewhat larger. Sorry about my oversight & thanks for explaining it. – John Omielan Jul 26 '19 at 19:32
  • 1
    @KeithReynolds As amd has explained, the answer involves extending one of the $2$ circles so it's radius is $e + f$ instead. Then the line joining those $2$ circles are tangent to both circles. As such, the solution involves solving for this tangent line (from which you can get it's angle with the $x$-axis), which has already been done several times on this site. I should've seen this earlier myself. – John Omielan Jul 26 '19 at 19:36
  • Thanks to both JohnOmielan amd. I also feel silly, because increasing the radius of one of the circles escaped me as well. Despite solving involves determining the line tangent to two circles has been covered, this question as it is, may be useful to others who also did not think of defining a new circle with radius e+f. – Keith Reynolds Jul 26 '19 at 19:48
  • 1
    For my part, I wouldn’t mark this as a duplicate, although it does reduce to a previously-answered question. – amd Jul 26 '19 at 19:50

1 Answers1

2

The simplest approach that comes to mind is to increase the radius of one of the circles by the wire thickness and then compute their common inside tangents. If you want to keep things symmetric, you could instead grow both circles by half the wire width. If you do the latter, then you’re effectively working with the wire’s centerline.

Questions about computing common tangents to two circles are pretty common here, so if you don’t know how to do that, a simple search will turn up many methods. This question came up near the top of my search just now. If you use the symmetric approach I mentioned above, since the two circles have the same radius, their inside tangents pass through the midpoint of the centers, so you can reduce the problem to that of finding tangents to a single circle through that point.

P.S. Using the symmetric construction, the angle can be computed directly. Setting $D$ to be the distance between circle centers and measuring angles clockwise, we have for the angle $\alpha$ of the line joining the two centers $$\cos\alpha = \frac{c-a}D \\ \sin\alpha = \frac{b-d}D.$$ If we’re wrapping clockwise around the top nail, we want to increase this by the angle $\beta$ between this line and the centerline of the wire, which, as noted above passes through the midpoint of the circle centers and is tangent to the circles with radius increased by $f/2$. We therefore have $$\sin\beta = {e+f/2\over D/2} = \frac{2e+f}D \\ \cos\beta = \sqrt{1-\sin^2\beta}.$$ Finding $\alpha+\beta$ then becomes a matter of applying any of the trigonometric sum-of-angles formulas and computing the inverse trig function. I don’t have a good feel for whether this is going to be more or less work than computing the tangent line.

amd
  • 53,693