What is the maximum of $\sum_{k=1}^{\infty} (-1)^k(^kx)$?

Question

During my testing of the series $\sum\limits_{k=1}^{n} (-1)^k(^kx)$, I found that the sum converges to two limits when $n \to \infty$, for $e^{-e} \lt x \le e^{1/e}$ and oscillates between depending on whether $n$ is even or odd.

Here, $^kx$ is tetration. The notation $^kx$ is the same as $x^{x^{x^{....}}}$, which is the application of exponentiation $k-1$ times. Ex. $^3x=x^{x^x}$.

Questions:

$(1)$ What is the maximum and minimum of $\lim\limits_{n\to \infty}\sum\limits_{k=1}^{n} (-1)^k(^kx)$ for even $n$?

$(2)$ What is the maximum and minimum of $\lim\limits_{n\to \infty}\sum\limits_{k=1}^{n} (-1)^k(^kx)$ for odd $n$?

Edit 1:

Also during my testing in PARI, I observed that the sum seems to converge to two values only in the domain of $e^{-e} \lt x \le e^{1/e}$. I think the reason for this maybe is that, since $^{\infty}x$ converges only for $e^{-e} \lt x \le e^{1/e}$, the sum also converges for the same domain. I would appreciate if someone could explain why the sum converges only for $e^{-e} \lt x \le e^{1/e}$.

Edit 2:

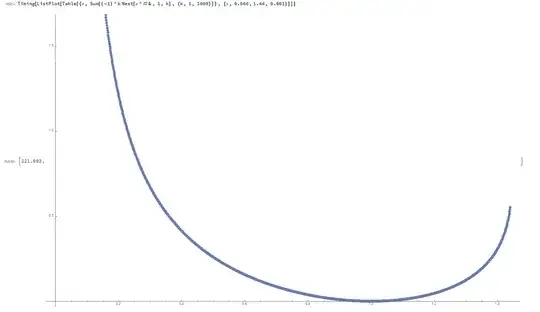
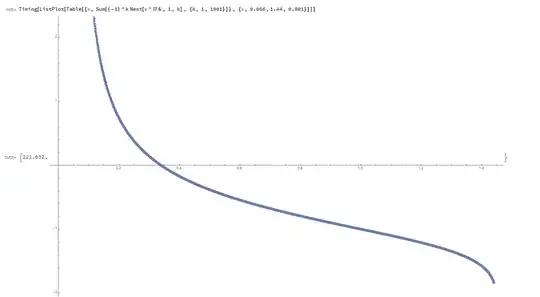
With the help of user Vepir, I was able to plot $\lim\limits_{n\to \infty}\sum\limits_{k=1}^{n} (-1)^k(^kx)$ for both even and odd $n$.

Even $n$:

Odd $n$:

Observations from graphs:

$(i.)$ $x=e^{-e}$ is the maximum for $\lim\limits_{n\to \infty}\sum\limits_{k=1}^{n} (-1)^k(^kx)$ for both even and odd $n$ when $e^{-e} \lt x \le e^{1/e}$.

$(ii.)$ $x=1$ is the minimum for $\lim\limits_{n\to \infty}\sum\limits_{k=1}^{n} (-1)^k(^kx)$ for even $n$ when $e^{-e} \lt x \le e^{1/e}$.

$(iii.)$ $x=e^{1/e}$ is the minimum for $\lim\limits_{n\to \infty}\sum\limits_{k=1}^{n} (-1)^k(^kx)$ for odd $n$ when $e^{-e} \lt x \le e^{1/e}$.

Now how can we prove any of the three claims above?

Answer 1

First of all, ${}^\infty x$ converges for $e^{-e}\color{red}{\leqslant}x\leqslant e^{1/e}$ (a good reference here is "Exponentials Reiterated" by R.A.Knoebel, mentioned in some posts on this site). But, indeed, both $s_{2n-1}(x)$ and $s_{2n}(x)$, where $s_n(x)=\sum\limits_{k=1}^{n}(-1)^k({}^k x)$, converge only for $e^{-e}<x\leqslant e^{1/e}$. To see why, let $e^{-e}\leqslant x\leqslant e^{1/e}$, $y={}^\infty x$ and ${}^n x=y(1-r_n)$. Then $r_{n+1}=1-y^{-r_n}$ and $$\lim_{n\to\infty}r_n=0\implies\lim_{n\to\infty}\frac{r_{n+1}}{r_n}=\ln y.$$ Thus, when $e^{-1}<y<e$ (i.e. when $e^{-e}<x<e^{1/e}$), both sums converge (by the ratio test). The convergence at $x=e^{1/e}$ follows from the fact that $r_n$ is positive and decreasing in this case. Finally, for $x=e^{-e}$ $$r_{n+1}=1-e^{r_n}\implies r_{n+2}=1-e^{1-e^{r_n}}=r_n-r_n^3/6+o(r_n^3)$$ from which one obtains $\lim\limits_{n\to\infty}(-1)^{n-1} r_n\sqrt{n}=\sqrt{6}$ (see this question for an approach). Thus, due to divergence of $\sum\limits_{n\geqslant 1}\frac{1}{\sqrt{n}}$, both $s_{2n-1}(e^{-e})$ and $s_{2n}(e^{-e})$ diverge to $+\infty$. This also proves $\color{blue}{(i.\!)}$.

The $\color{blue}{(ii.\!)}$ and $\color{blue}{(iii.\!)}$ are easy. The (elementary) observation made in the article, \begin{align} x<1&\implies x<{}^3 x<{}^5 x<\ldots<{}^6 x<{}^4 x<{}^2 x; \\ x>1&\implies x<{}^2 x<{}^3 x<\ldots, \end{align} gives $s_{2n}(x)>0[{}=s_{2n}(1)]$ when $x\neq 1$, proving $\color{blue}{(ii.\!)}$, and $s_{2n-1}(x)>-1[{}=s_{2n-1}(1)]$ when $x<1$. Finally, for $x>1$, ${}^{n+1}x-{}^n x$ is increasing, which is proven using induction on $n$ and $${}^{n+1}x-{}^n x={}^n x(x^{{}^n x-{}^{n-1}x}-1).$$ Thus, $s_{2n-1}(x)$ is decreasing (at least) for $x>1$, proving $\color{blue}{(iii.\!)}$.