Problem to understand $\mathbb R^2$. Does $(x,y)$ depend on a basis?

Question

I know that $$\mathbb R^2=\{(x,y)\mid x,y\in\mathbb R\}.$$ Now, I'm having a truble to understand properly $(x,y)$. So, everyone will be agree that $$(x,y)=x(1,0)+y(0,1).$$

But what are exactly $(1,0)$ and $(0,1)$ ? Because, if I have to see $\{(1,0),(0,1)\}$ as a basis, it can be any basis... Just take $\mathcal V=\{v_1,v_2\}$ and $\mathcal W=\{w_1,w_2\}$ two differents basis. So w.r.t. $\mathcal W$, $w_1=(1,0)$ and $w_2=(0,2)$. Also, w.r.t. $\mathcal V$, $v_1=(1,0)$ and $v_2=(0,2)$, but of course, $w_1\neq (1,0)$ and $w_2=(0,1)$. But as we can see, $\{(1,0),(0,1)\}$ can be identify to any basis of $\mathbb R^2$.

I agree that if I'm in $\mathcal V$, I shouldn't write $v_1=(1,0)$ but rather $[v_1]_{\mathcal V}=(1,0)$. So I abuse slightly notation.

But when I write $$\mathbb R^2=\{(x,y)\mid x,y\in\mathbb R\},$$ when I take $(x,y)\in\mathbb R^2$, I take it independently to any basis (since a vector space doesn't depend on a basis)... So, when I write $(x,y)=x(1,0)+y(0,1)$ what are $(1,0)$ and $(0,1)$ ?

Just to illustrate my point. If I represent $\mathbb R^2$ like that

the the vector $(0,1)$ is $e_2$, but if I represent $\mathbb R^2$ like that

the vector $(0,1)$ is $v_2$ which is very different that $e_2$ (much longer and not in the same sens).

Answer 1

You have to be careful to distinguish between a set of elements and the basis for it. The fact

$$\mathbb{R}^2=\{(x,y)∣x,y \in \mathbb{R}\}$$

describes a set of elements and is just a definition. It doesnt care about any base!

Now if you want to do computation with its elements, a basis (that is a one to one connection between scalars and the elements) is nice to have.

You can use any basis you want, but most of the time the canonical basis (1,0) and (0,1) is used just to make computations easier.

Answer 2

Your question "What exactly are $(0,1)$ and $(1,0)$?" leads me to think that you have some doubt about the very basic concept of an ordered pair, so let me address that point first.

The ordered pair is a concept of set theory, which is governed by a simple law: for each $r$, $s$ there exists a unique ordered pair $(r,s)$ having the property that for any $r,s,t,u$, the equation $(r,s)=(t,u)$ is true if and only if both of the equations $r=t$ and $s=u$ are true.

One can also use ordinary set notation to define ordered pairs: $$(r,s) = \{\{r\},\{r,s\}\} $$

Once you've settled on your understanding of ordered pairs, $\mathbb R^2$ is defined to be the set of all ordered pairs $(x,y)$ such that $x \in \mathbb R$ and $y \in \mathbb R$.

Beyond those set theoretical issues, it seems that what you have discovered is that $\mathbb R^2$ has many different coordinate systems. First of all, there is the "standard" coordinate system where the first coordinate of $(x,y)$ is $x$ and the second coordinate of $(x,y)$ is $y$. However, there are in fact many different coordinate systems, one for each invertible matrix of real numbers $\begin{pmatrix} a & b \\ c & c \end{pmatrix}$, where the first coordinate of $(x,y)$ are given by the two entries of the matrix product $$(x,y) \cdot \begin{pmatrix} a & b \\ c & d \end{pmatrix} = (xa+yc,xb+yd) $$ so the first coordinate is $xa+yc$ and the second is $xb+yd$. I want to strongly emphasize a point here: in this new coordinate system, the coordinates of $(x,y)$ do not have to be either $x$ or $y$.

In fact, if you can follow these computations then you'll see that you can get an example just like your second picture: the coordinate system using the basis $(1,0)$ and $(4,1)$ can be obtained by using the matrix $$\begin{pmatrix} 1 & 0 \\ -4 & 1 \end{pmatrix} $$ Try it out! You'll see that in the coordinate system given by this matrix one has: the first coordinate of $(1,0)$ is $1$ and the second coordinate is $0$; whereas the first coordinate of $(4,1)$ is $0$ and the second coordinate is $1$.

Answer 3

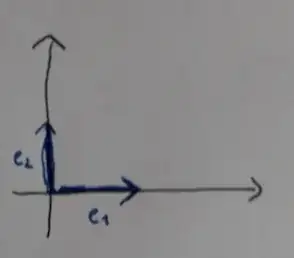
It seems to me that the basic confusion is that you identify $\mathbb{R}^2$ too strongly with the space of geometric vectors in the plane. These spaces are not the same. Geometric vectors are simply “arrows”, while vectors in $\mathbb{R}^2$ are nothing but pairs of real numbers: $(x,y)$ where $x \in \mathbb{R}$ and $y \in \mathbb{R}$.

So when you ask what $(1,0)$ really is, the answer is that it's the pair of real numbers whose first member is the number $1$ and whose second member is the number $0$. That's all!

On the other hand, it's true that if you pick a basis for the space of geometric vectors in the plane (that is, two linearly independent “arrows”), then any geometric vector can be represented by a unique element $(x,y)$ in $\mathbb{R}^2$ (where $x$ and $y$ are the coordinate of the vector with respect to the chosen basis). But the correspondence between geometric vectors and elements in $\mathbb{R}^2$ of course depends on the choice of basis.

So far it's pretty easy, but many students become confused when one does the same thing in the space $\mathbb{R}^2$ itself. Namely, if you pick a basis for $\mathbb{R}^2$ (that is, two linearly independent pairs of numbers), then any element $(a,b)$ in $\mathbb{R}^2$ can be represented by a unique element $(x,y)$ in $\mathbb{R}^2$. And $(x,y) \neq (a,b)$, unless the basis is the standard basis consisting of the vectors $(1,0)$ and $(0,1)$. So each vector in $\mathbb{R}^2$ is represented by some other vector in $\mathbb{R}^2$.

One way to (possibly) reduce the risk of confusion is to use column matrices for coordinates, so that if $\mathbf{v} = x_1 \mathbf{e}_1 + x_2 \mathbf{e}_2$, then you write the coordinate vector for $\mathbf{v}$ (with respect to the basis consisting of the vectors $\mathbf{e}_1$ and $\mathbf{e}_2$) as the column matrix $$ \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} , $$ rather than as the pair $(x_1,x_2)$.

For example, if we do this in $\mathbf{R}^2$ with the basis $\mathbf{f}_1=(1,1)$ and $\mathbf{f}_2=(2,3)$, then the vector $$ \mathbf{v} = (12,17) = 2(1,1) + 5(2,3) = 2 \mathbf{f}_1 + 5 \mathbf{f}_2 $$ has the coordinate vector $$ \begin{bmatrix} 2 \\ 5 \end{bmatrix} $$ with respect to that basis.

But if we take the standard basis, $\mathbf{e}_1 = (1,0)$ and $\mathbf{e}_2 = (0,1)$, then the same vector $$ \mathbf{v} = (12,17) = 12(1,0) + 17(0,1) = 12 \mathbf{e}_1 + 17 \mathbf{e}_2 $$ is represented by the coordinate vector $$ \begin{bmatrix} 12 \\ 17 \end{bmatrix} $$ instead.

In both cases, $\mathbf{v}$ itself really is just the number pair $(12,17)$, but its coordinate vector depends on which basis you use.

Answer 4

The point is that the Cartesian product $\Bbb R \times \Bbb R$ can be naturally equipped with a vector space structure.

First you have to define the addition of any two elements in $\Bbb R \times \Bbb R$ so that an abelian group is formed.

Next, you have to define scalar multiplication. You select $\Bbb R$ to be the field, and need a definition:
for $\lambda \in \Bbb R$ and $v \in \Bbb R \times \Bbb R$ you have to associate an element (called a vector) $\lambda v \in \Bbb R^2$.

Finally, you have to show that what you have created satisfies the properties/axioms of a vector space.

So when you write, say $(3,0) = 3 (1,0)$, you are simply saying that the element $(3,0)$ in the abelian group $\Bbb R^2$ can also be written as the scalar $3$ in the field $\Bbb R$ times the vector $(1,0)$ in $\Bbb R^2$.

Note that the definition of a vector space comes before we can define what it means for two vector to be linearly independent and ...

Answer 5

Let $B_1= \{(1,0,)(0,1)\}$ and $B_2 = \{(2,0),(0,2)\}$ be two basis for $\mathbb{R}^2$. As you pointed out, if $x \in \mathbb{R}^2$ is a vector, then the coordinates it has on each basis differ. For example, if $x=(1,1)$ is your vector and $B_1$ is your basis, then it means that $x= 1 \cdot (1,0) + 1 \cdot (0,1)$. However, this same vector is written as $x=(\frac{1}{2},\frac{1}{2})$ on $B_2$. Still, they are the same vector, only on different coordinates system. Geometrically they may seem different, but you could think that they are just been measured differently.

Note, also, that even the angle of the vector may vary: If I take $B_3 = \{(1,0),(1,1)\}$, then the coordinates of $x$ on $B_3$ are $2$ and $1$. Still, we are talking about the same vector, only measured under new perspectives.

In these cases, it can be helpful to make use of some new notation: If I'm talking about $x$ on the first basis, then I could write $[x]_{B_1}$, $[x]_{B_2}$ for the second case, and so on.

Usually, the basis I've called $B_1$ is referred to as the canonical basis of $\mathbb{R}^2$, and the vector here are the most natural ones.

I don't know if this really answer the question but, if not, please comment here, so that I can try again.