I understand why the derivative of $\sin x$ is $\cos x$, and why the derivative of $\cos x$ is $-\sin x$ in a geometric way.
But I can not understand why the derivative of $\tan x$ is $\sec^2 x$.
Can someone please explain this in a visual, geometric way using the unit circle?
The following is maybe a little bit hand-wavy, but the idea is hopefully clear.
If $\theta$ is the angle $EAH$ in the figure, then $\tan \theta$ is the lenght of the segment $BC$. If we increase that angle slightly (or “infinitesimally”), then the segment $EF$ is approximately $d\theta$, and we would like to know the length of $CD$, since that's the change in $\tan \theta$.
Since the triangle $AHE$ is $\cos \theta$ times smaller than the triangle $ABC$, the segment $EF$ is $\cos \theta$ times shorter than $CG$. And $CG$ is in turn $\cos \theta$ times shorter than $CD$ (similar triangles; the angle $GCD$ is $\theta$ and the angle $CGD$ is $\pi/2$ up to an infinitesimal correction). So $EF$ is $\cos^2 \theta$ times shorter than $CD$, and thus $$ d( \tan\theta ) = CD = \frac{EF}{\cos^2\theta} = \frac{d\theta}{\cos^2 \theta} . $$
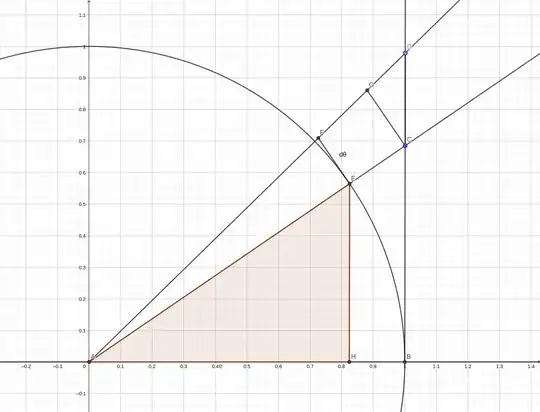
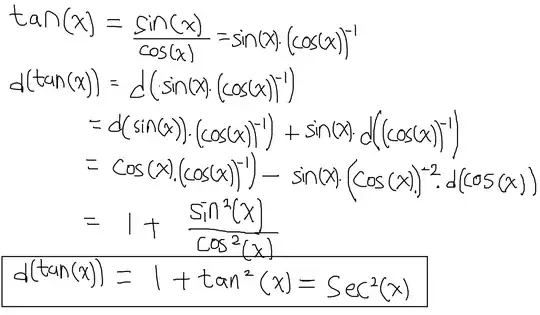First, look at the graph of $\tan(x)$.
It has vertical asymptotes at integer multiples of $\dfrac{\pi}{2}$ and is undefined at $-\dfrac{\pi}{2}$ and $\dfrac{\pi}{2}$. Observe that from $-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$, the slope of $\tan(x)$ is always increasing. Notice that it increases faster from $-\dfrac{\pi}{2} \leq x \leq -\dfrac{\pi}{4}$ and from $\dfrac{\pi}{4} \leq x \leq \dfrac{\pi}{2}$. Then, let's take a look at the graph of $\sec^2(x)$.
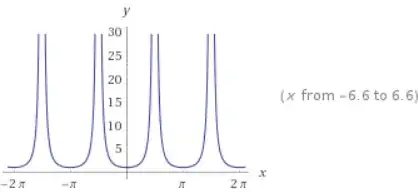
Observe that $\sec^2(x)$ is always positive as the slope of $\tan(x)$ was always positive. Also observe that $\sec^2(x)$ has vertical asymptotes at integer multiples of $\dfrac{\pi}{2}$. If we zone in on $-\dfrac{\pi}{2} \leq x \leq \dfrac{\pi}{2}$, then we see that the value of $\sec^2(x)$ is greater as we approach $x=-\dfrac{\pi}{2}$ or $x=\dfrac{\pi}{2}$. This is because we can think of the derivative as slope and previously saw that the slope was greatest near the asymptotes.
Therefore, it is natural for $\sec^2(x)$ to be the derivative of $\tan(x)$. The same technique will work for $\sin(x), \cos(x)$, and many others. If you are uncomfortable with the algebra then it is best draw a function and its derivative on graph paper.
Use the definition of derivative and the rule $\tan(a+b) =\dfrac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)} $.
Then
$\begin{array}\\ \tan(x+h)-\tan(x) &=\dfrac{\tan(x)+\tan(h)}{1-\tan(x)\tan(h)}-\tan(x)\\ &=\dfrac{\tan(x)+\tan(h)-\tan(x)(1-\tan(x)\tan(h))}{1-\tan(x)\tan(h)}\\ &=\dfrac{\tan(h)+\tan^2(x)\tan(h)}{1-\tan(x)\tan(h)}\\ \text{so}\\ \dfrac{\tan(x+h)-\tan(x)}{h} &=\dfrac{\tan(h)+\tan^2(x)\tan(h)}{h(1-\tan(x)\tan(h))}\\ &=\dfrac{\tan(h)}{h}\dfrac{1+\tan^2(x)}{1-\tan(x)\tan(h)}\\ &\to 1+\tan^2(x)\\ &= 1+\dfrac{\sin^2(x)}{\cos^2(x)}\\ &= 1+\dfrac{\sin^2(x)}{\cos^2(x)}\\ &= \dfrac{1}{\cos^2(x)}\\ &=\sec^2(x)\\ \end{array} $
since, as $h \to 0$, $\dfrac{\tan(h)}{h} \to 1$ and $\tan(h) \to 0$.
The easiest way to derive this would be the quotient rule, the other way is looking at the graph just like what Axion posted. I dont know how to derive it with unit circle/geometry way, sorry :) . But, instead of quotient rule i will just use product rule which is a bit inefficient because $cos(x)$ is in denominator (and i have to use chain rule for that), and it will do the trick anyway. So as you can see below the derivative of $tan(x)$ is just itself squared and the added by one, which by identities become $sec^{2}(x)$.
Edit : i just found the geometric way, please take a look on this post : Geometric Proof that $\frac{d}{d\theta}(\tan{\theta}) = 1 + \tan^{2}{\theta}$
I can't explain it geometrically, but I can prove it algebraically:
$$\begin{aligned} \frac{d}{dx} [\tan x] &= \frac{d}{dx} \left[\frac{\sin x}{\cos x} \right] &\quad \text{Definition of } \tan x\\ &= \frac{\frac{d}{dx}[\sin x]\cdot (\cos x) - (\sin x) \cdot \frac{d}{dx} \left[\cos x \right]}{\cos^2 x} &\quad \text{Quotient Rule}\\ &= \frac{\cos^2 x + \sin^2x }{\cos^2 x} &\quad \text{Derivatives of } \sin x \text{ and } \cos x \\ &= {\frac{1}{\cos^2x}} &\quad \text{Pythagorean Identity} \\ &= {\sec^2 x} & \end{aligned}$$
You need to apply the quotient rule to $$\tan x =\frac {\sin x }{\cos x }$$
$$ (\tan x )'= \frac {(\sin x )' (\cos x) -(\sin x)(\cos x )'}{(\cos x )^2}=$$
$$ \frac {(\cos x ) (\cos x) -(\sin x)(-\sin x )}{(\cos x )^2} =$$
$$\frac {1}{\cos ^2 x} = \sec ^2 x$$
