As my title suggests, the last few lines of the proof to the following theorem:
If $a=bq+r$, then $gcd(a,b)=gcd(b,r)$
are not sitting well with me. I understand completely the preceding remarks in the proof...namely:
$x|a \land x|b \Rightarrow x|r$
and
$x'|b \land x'|r \Rightarrow x'|a$
However, I fail to see that this implies $x'$ and $x$ belong to the same set...which is the crucial 'insight' that precedes the ultimate steps of proving the theorem.
I've tried a few different ways of visualizing these sets...specifically:
Let $D = \{d\ \epsilon \ \mathbf Z | \ \ d|a \}$ i.e. $D$ is the set of all divisors of $a$
Let $E = \{e\ \epsilon \ \mathbf Z | \ \ e|b \}$ i.e. $E$ is the set of all divisors of $b$
Let $F = \{f\ \epsilon \ \mathbf Z | \ \ f|r \}$ i.e. $F$ is the set of all divisors of $r$
Let $G = D \cap E$
Let $H = E \cap F$
Therefore:
if $x|a \land x|b$, then $x \ \epsilon \ G $
and
if $x'|b \land x'|r$, then $x' \ \epsilon\ H$
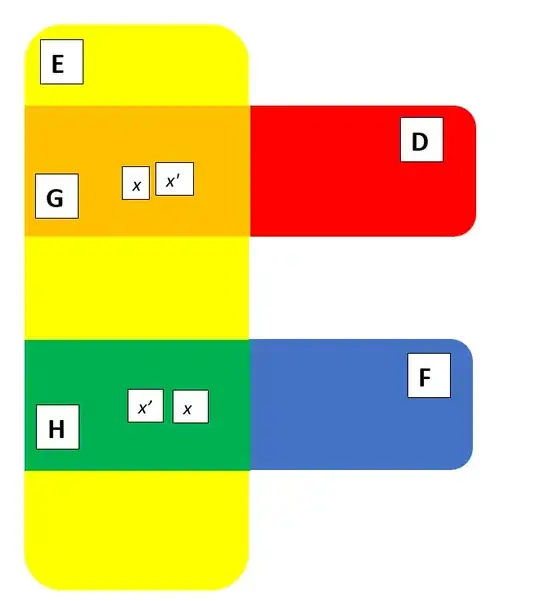
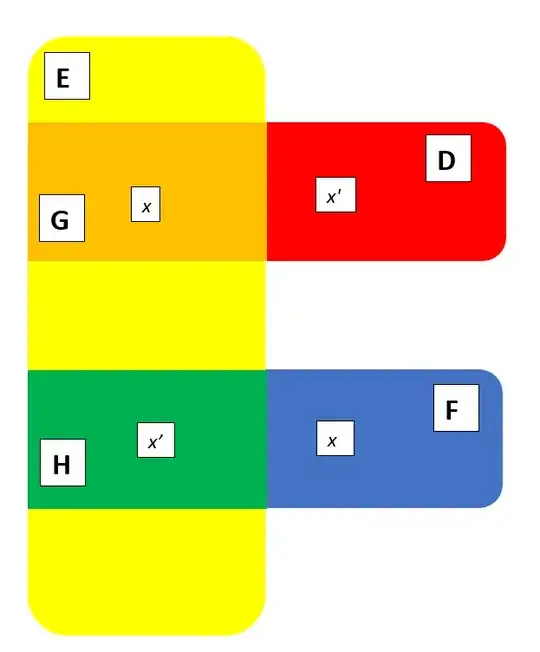
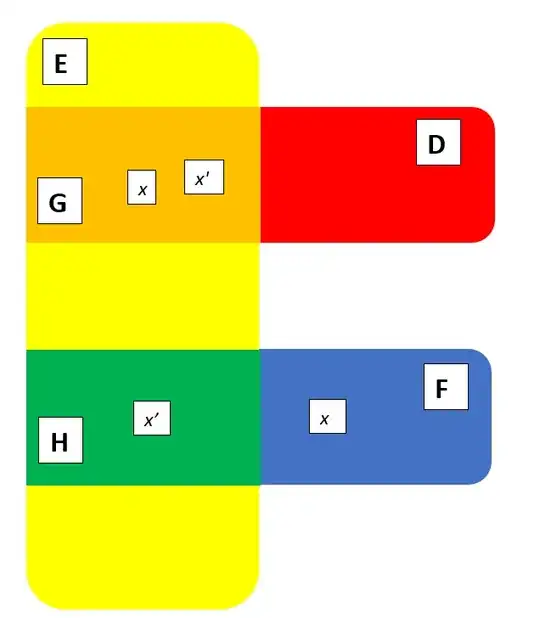
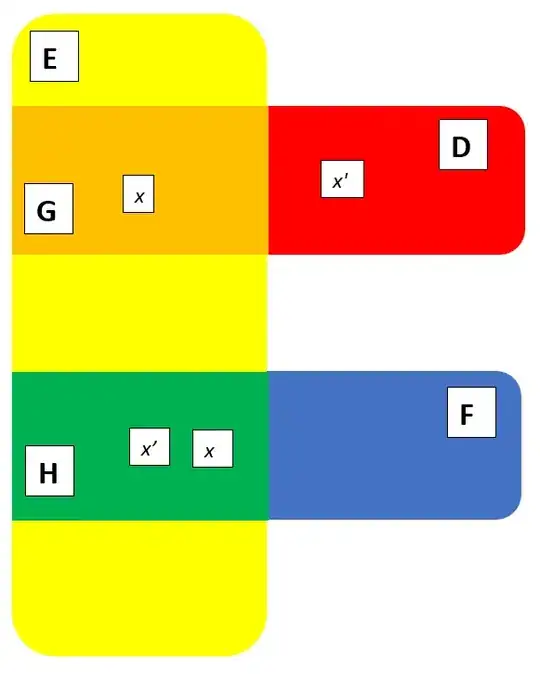
I note that $x'$ and $x$ are clearly both in the set $E$, as they are both divisors of of $b$. Additionally, by my first two remarks:
$x\ \epsilon \ F$ and $x'\ \epsilon\ D$
This generates the resulting odd illustration, where both $x$ and $x'$ need to be simultaneously present in two different locations (which I have depicted as occurring in one of four possible different ways):
(Sorry for all of the pictures). So, obviously, these elements can't be in two places at once. To me, intuitively, the only way this can actually (within the limits of the rule you can only be in one place at a time) happen is if the set containing $x$ is identically the same set that contains $x'$. Unfortunately, I am uncomfortable with that statement. Is there a proof of what I am regarding as "intuitive"? Further, does this mean that the set $G$ and the set $H$ are the same set even though they are fundamentally constructed in different ways? Such a situation could be expressed by the following picture:
However, I am still uncertain of whether or not I can "accept" this based purely on the idea of its visual appeal. Any help would be appreciated!