$\int_0^1 \lfloor -x\rfloor \,dx$

Question

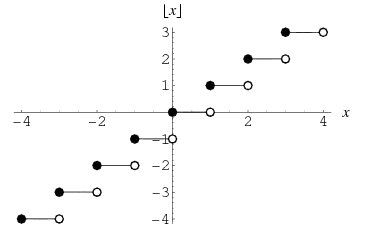
Find: $$\int_0^1 \lfloor -x\rfloor \,dx$$

I tried solving the question but got stuck along the way. Here, as usual, $\lfloor x\rfloor$ denotes the floor function, and in my solving, I treated the negative symbol like usual. Is it wrong? Then how to calculate this problem? Help me thank you.

Note: I have reformatted the post to use the standard notation, $\lfloor x\rfloor$, for the floor function. If you preferred to do it the other way, you can roll back or modify the edit. — lulu, Jul 20 '19 at 12:23
This can help: https://math.stackexchange.com/a/1980521/669687. — Monadologie, Jul 20 '19 at 12:32

score 4 · Answer 1 · answered Jul 20 '19 at 12:27

4

On the open interval $(0,1)$ your function becomes $-1$. So this problem is equivalent to solving $\int_0^1 -1 \;\text{d}x$

answered Jul 20 '19 at 12:27

Ruben

2,082

Is it continous in [0,1)? – F1166 Jul 20 '19 at 12:52
@F1166 No, the function is $0$ at $0$. – Ruben Jul 20 '19 at 12:56
2

@F1166 you can ignore finitely many discontinuities anyway. – Henno Brandsma Jul 20 '19 at 14:23
@HennoBrandsma ecaxtly – Ruben Jul 20 '19 at 14:56

Axion004 · Answer 2 · 2019-07-23T03:59:57.183

Another way to think about this integral is to consider the form

$$\int_{-n}^0 \lfloor x\rfloor \ dx$$

which can be visualized by the step function

The area underneath this function from $-x$ to $0$ is

$$ -x -(x+1) -(x+2) - \dots -3 -2 -1 $$

Now, since

$$\int_{-n}^0 \lfloor x\rfloor \ dx = \int_{0}^n \lfloor -x\rfloor \ dx$$

and

$$\int_{-n}^0 \lfloor x\rfloor \ dx = \sum_{k=1}^n (-k)=-\frac{1}{2}n(n+1)$$

We see that

$$\int_{-1}^0 \lfloor x\rfloor \ dx = -\frac{1}{2}(2) = -1 = \int_{0}^1 \lfloor -x\rfloor \ dx$$

$\int_0^1 \lfloor -x\rfloor \,dx$

2 Answers2