5

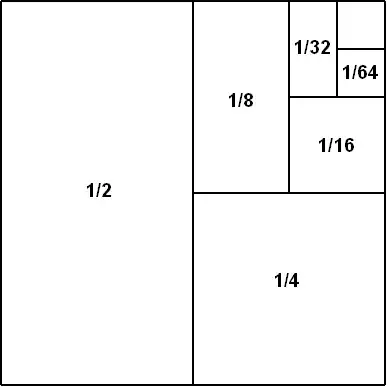
This is a visual proof for the sum of the reciprocals of powers of 2 -

enter image description here

Are there a similar proofs for reciprocals of square and triangular numbers?

I couldn't find any.

I don't know if I used the right terms; maybe it's: infinite series sum.

So correct this question if it's wrong.

Blue
  • 75,673
About Blank
  • 51
  • 3
    For triangular numbers, notice that $$\sum_{n=1}^{\infty} \frac 1 {T_n} = 2 \sum_{n=1}^{\infty} \frac 1 {n(n+1)} = 2 \sum_{n=1}^{\infty} \left ( \frac 1 n - \frac 1 {n+1} \right )$$ so you might want to look for visual proofs that the sum of the telescoping series is $1$. – Luca Bressan Jul 16 '19 at 08:47
  • 1
    For the reciprocal of squares, this seems unlikely as the sum is a transcendental number, hence not constructible. –  Jul 29 '19 at 12:16
  • 1
    The reciprocal of the squares can be visualized (and in a clumsy way) in $3D$ I think, and never in $2D$. Start by drawing a cube with side of length $1$ then above it at its corner, draw a box of the same height $1$ but of a square face with length $\frac{1}{2}$ (it'll have the volume of $\frac{1}{4}$) and above it a box of height $1$ also and width=length$=\frac{1}{3}$ and so on ... – Fareed Abi Farraj Jul 29 '19 at 13:05
  • Luca Bressan - something like this - for triangular numbers? But probably not exactly; this looks as relating to harmonic-numbers. http://demonstrations.wolfram.com/SumOfATelescopingSeriesII/#snapshot1 – About Blank Jul 29 '19 at 16:32

0 Answers0