0

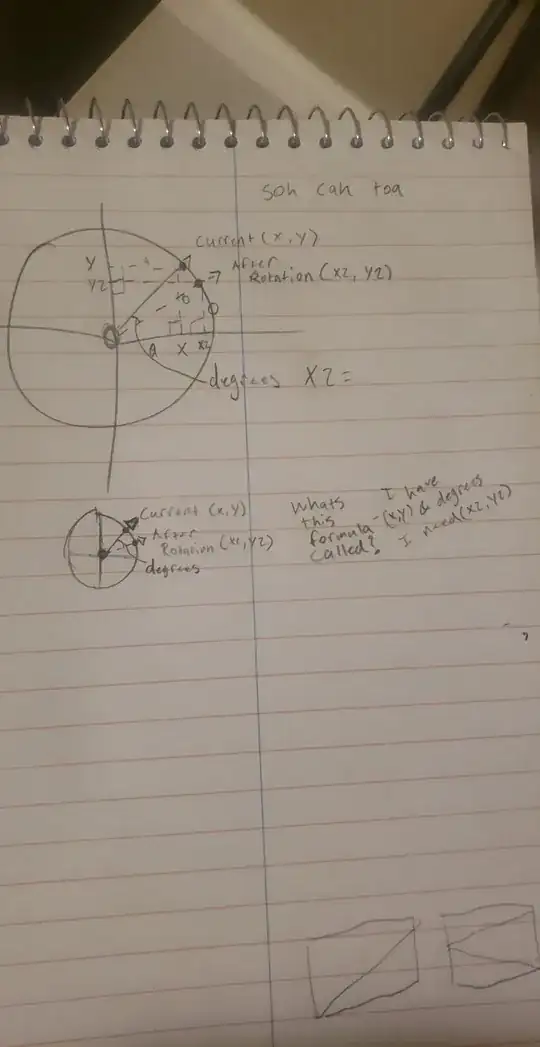
I have

  • center of circle's $x_1, y_1$ (called the eye in my code)
  • degrees
  • current $x_2, y_2$ (coordinates on the circle)

I want to add degrees to the $x_2, y_2$ and get the new "$x_3, y_3$"

Side Note: I dropped out of school and never learned TRIG. So a simple explanation would do wonders.

enter image description here

nmasanta
  • 9,222
Brayan Byrdsong
  • 1
  • 2
    What exactly are $;x,y;$ ? Is it an ordered pair $;(x,y);$ which is the center of some circle, or something else? And anyway: what does "adding degrees " to point in the plane (or whatever) is? – DonAntonio Jun 30 '19 at 07:31
  • I added an image, hopefully that helps – Brayan Byrdsong Jun 30 '19 at 07:37
  • 1
    You use $x,y$ twice. Once it looks like the center of the circle, and once it looks like a point on the circle. Please clarify. It sounds like you have the center of a circle $(x,y)$, a point on the circle $(x_1,y_1)$ and want to find another point on the circle $(x_2,y_2)$ that is a given angle (clockwise, counterclockwise, do you care?) from the first point. Is this right? Stating the problem clearly is usually the first step to a solution. – Ross Millikan Jun 30 '19 at 07:37
  • See https://math.stackexchange.com/questions/814950/how-can-i-rotate-a-coordinate-around-a-circle. I think that's exactly what you're looking for. – Saswat Padhi Jun 30 '19 at 07:39
  • Ok, the drawing did help to make clear your intention: you want to rotate the circle on its center to get from a given point on it another point on it...yet I, at least, can't see how to achieve that without some minimal trigonometry and/or linear algebra... – DonAntonio Jun 30 '19 at 07:40
  • First time using stackoverflow, edited it – Brayan Byrdsong Jun 30 '19 at 07:40
  • Yes, show me the minimal Trig, I was just stating I don't know this stuff. – Brayan Byrdsong Jun 30 '19 at 07:42
  • Then read the linked question and answer by Saswat, above – DonAntonio Jun 30 '19 at 07:42
  • 1
    It WORKS! Thanks my guys. – Brayan Byrdsong Jun 30 '19 at 08:02

0 Answers0