In this picture: a runner wants reach B by starting at A. Velocity in White space is $10 m/s$ and in brown space is $5 m/s$. what is the minimum time that he need? I upload original image of question but it wrote in Farsi. Assume that Brown region is a an unbounded band along the $y$ axis.
$$a)\sqrt{26}$$ $$b)\sqrt{20}$$ $$c)5$$ $$d)\sqrt{30}$$ $$e)\sqrt{34}$$
None of the provided answers are correct. The minimum time is an algebraic number of degree 8, as I will show.
Model the problem such that the runner starts at the origin, $B=(40,30)$ and the slow strip is $20<x<30$. Now let the runner meet the slow strip at $(20,a)$ and exit it at $(30,b)$, with straight lines in between. The time taken is then $$s=\newcommand{hypot}{\operatorname{hypot}}\frac{\hypot(20,a)}{10}+\frac{\hypot(10,b-a)}5+\frac{\hypot(10,30-b)}{10}$$ I turned this into a polynomial expression in $a,b,s$, then using techniques very similar to those used in another answer of mine, derived minimal polynomials for the three variables: $$s^8-68s^6+5266s^4-177036s^2+845325=0;s=6.121773\dots$$ $$27a^4-1080a^3+24800a^2-576000a+5760000=0;a=17.661784\dots$$ $$27b^4-2700b^3+103400b^2-1758000b+11070000=0;b=21.169107\dots$$
I assume that runner moves like this picture:
Calculating time of moving:
$$t=\frac{d_{1}}{10} + \frac{d_{2}}{5}+\frac{d_{3}}{10}=\frac{d_{1}+d_{2}+d_{3}}{10}+\frac{d_{2}}{10} $$
we know that $d_{1}\ge20$, $d_{2}\ge10$ and $d_{3}\ge10$ Also : Direct path between $A$ and $B$ has the minimum length: So $d_{1}+d_{2}+d_{3}\ge AB$. And $AB=50$
$$ t \ge \frac{AB}{10}+1\ge 6$$
So minimum time is at least $6$.
If I move horizontally in brown region, absolutely it take more than $6$ seconds.
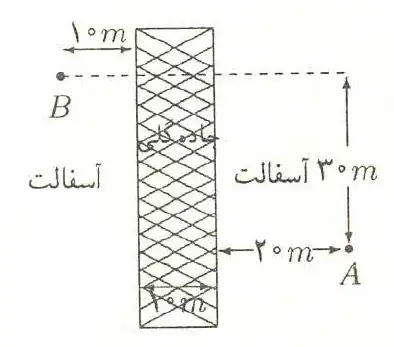
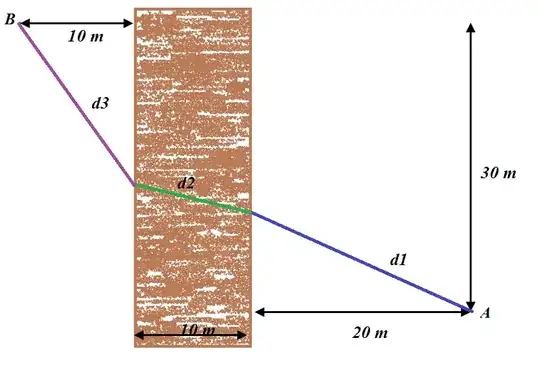
That would be the same path that a light ray would take, through media with different refractive indices.
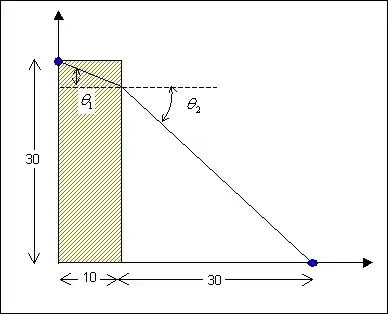
Without loss of generality, we can move the "sand" stripe to start at B. Then the optical analogy will tell us that the refractive index of "sand" is $2$ and that $$ \sin \theta _{\,2} = 2\sin \theta _{\,1} $$
Without going into precise calculations, we can consider that
$$
3/4 < \tan \theta _{\,2} < 1
$$
so that $\theta _{\,1} $ will be approximately $\pi / 8$ , which means $ \tan \theta _{\,1} \approx \sqrt{2}-1 \approx 0.4$.
Therefore the path will enter the sand strip about $4$ m below $B$.
The time is then approximately $$ t \approx {{\sqrt {100 + 16} } \over 5} + {{\sqrt {900 + 26^{\,2} } } \over {10}} \approx {{11} \over 5} + {{40} \over {10}} \approx 6.2 \approx \sqrt {38} $$ and yes, $\sqrt {34}$ looks to be too low.
Note that the path that goes straight up at $45^\circ$and then horizontally across the "sand" would take $$ t = {{10} \over 5} + {{\sqrt {1800} } \over {10}} = 2 + 3\sqrt 2 = 6.24 $$ while the straight line from $A$ to $B$ would take $$ t = {{\sqrt {100 + 900/16} } \over 5} + {{30\sqrt {1 + 9/16} } \over {10}} = {{50} \over {20}} + {{150} \over {40}} = {{250} \over {40}} = 6.25 $$
-- notes --
The optical analogy helps in saying that, the piecewise path from A to B which attains the minimum time to be traversed shall obey to the Refraction Law $$ {{\sin \theta _{\,1} } \over {\sin \theta _{\,2} }} = {{v_{\,1} } \over {v_{\,2} }} = {{n_{\,2} } \over {n_{\,1} }} $$ which is valid also for mechanical particles (and for humans).
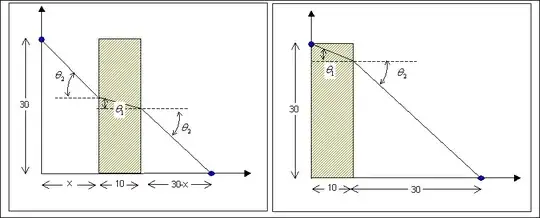
Since the above law is bidirectional, then we will have the situation depicted in this sketch, to confirm that the horizontal placement of the sand strip is ininfluential on the total time.
The exact solution will translate into finding the solution to $$ \eqalign{ & 10\tan \theta _{\,1} + 30\tan \theta _{\,2} = 30\quad \Rightarrow \cr & \Rightarrow \quad 10{{\sin \theta _{\,1} } \over {\sqrt {1 - \sin ^{\,2} \theta _{\,1} } }} + 30{{2\sin \theta _{\,1} } \over {\sqrt {1 - 4\sin ^{\,2} \theta _{\,1} } }} - 30 = 0 \cr} $$ which leads to a 4-th degree equation, as already evidenced in a previous answer.
Traversing the sand stripe takes the same amount of time as traversing twice as much white area, so if we replace the sand with a white stripe of twice the width, it will take the same amount of time to cross. $t = \sqrt{30^2+50^2}/10=\sqrt{34}$, or answer (e).
