Assume the IVP: \begin{cases} z^2 z_x + z_y = 0 \\ z(x,0) = f(x) \\ \end{cases}
The condition of existence of (locally) unique solution is: $$ P(t_0) \frac{dy(t_0)}{dt} - Q(t_0) \frac{dx(t_0)}{dt} \neq 0 $$ on the curve $(t,0,f(t))$, which holds true since:
$$ 0 - 1 \cdot 1 = -1 \neq 0 $$
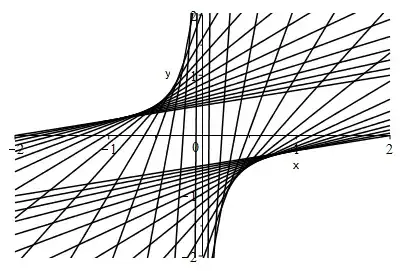
If we let $f(x) = x$, the solution is: $$ z = x - z^2 y \iff z(x,y) = \frac{-1 + \sqrt{1 + 4xy}}{2y} $$
Shock waves:
By the Implicit Function Theorem, the solution exists and is implicitly defined as long as: $$ 1 + f'(x - z^2 y)2zy > 0 $$ So a shock wave forms when: $$ 1 + f'(x - z^2 y)2zy = 0 \iff z = \frac{-1}{2y} \iff 1 + 4xy = 0 $$ Thus, the solution is uniquely defined for $1 + 4xy > 0$ and the region of shock is $1 + 4xy \leq 0$.
Question: Is the aforementioned an adequate description when someone wants to determine the regions where the solution is uniquely defined and the shock regions?