I am reading this post that proves why $\max\{0,x\}$ is not differentiable. But why $(\max\{0, x\})^n$ for $n>1$ is differentiable?
Asked
Active
Viewed 578 times
5
-
Well compute the the differential quotient, then you'll see – Severin Schraven Jun 24 '19 at 18:58
-
Do you mean $(max(0,x))^n$? – PCeltide Jun 24 '19 at 18:59
-
3For the very same reason why $|x|$ isn't differentiable at 0, but $|x|^n$ is, for $n>1$. A good exercise is to follow the reasoning in the post you linked to show that both left and right side differential limits coincide at $x=0$. One can show that straight from the definition of derivative. – Wham Bang Shang-a-Lang Jun 24 '19 at 18:59
4 Answers
3
Let $f_n(x) = max\lbrace 0, x\rbrace^n$ for some $n>1$, and the domain of the function is $\mathbb{R}$.
(edit) i.e. it is the piecewise function:
$$f_n(x) = \cases{0 & x $\leq$ 0 \\ x^n &x > 0}$$
It is clear that $f_n(n)$ is continuous over the domain by construction .
Note that for $x > 0$, the derivative of $f_n(x)$ exists and is $f_n'(x) = nx^{n-1}$.
For $x < 0$, the derivative is trivially 0. All that is left is to verify that the function is differentiable at $x=0$, and we are finished.
By definition, a function $g(x)$ is differentiable at a point $x_0$ if the limit $\lim_{x_n \rightarrow x_0} \frac{g(x_n - x_0) - g(x_0)}{x_n - x_0}$ exists. An equivalent definition is $\lim_{x_n \rightarrow x_0^+} \frac{g(x_n - x_0) - g(x_0)}{x_n - x_0} = \lim_{x_n \rightarrow x_0^-} \frac{g(x_n - x_0) - g(x_0)}{x_n - x_0}$ (i.e. the limit approaching from the left is equal to the limit approaching from the right).
You can show that the left-hand and right-hand limit are both equal to 0 directly.
(edit for clarification) If the derivative exists for a function g(x) for some point $x_0$, then the left hand limit and right hand limit at that point are equal to the derivative $g'(x_0)$.
Since the derivative of $x^n$ at $0$ (for $n > 1$) is 0 always, the right-hand limit is of our derivative is 0. Similarly, since the derivative of $0$ is $0$, the left-hand limit is 0.
Thus, the right-hand and left-hand limits are equal, which means the derivative exists at that point. With that, we have shown that the derivative exists for every point in $\mathbb{R}$.
Autho
- 46
-
If you want some more fun functions which are "strange", prove the following:
Prove $f(x) = \cases{xsin(\frac{1}{x}) & if $x \neq 0$\ 0 & else}$ is continuous everywhere. Next, prove that $f(x) = \cases{x^nsin(\frac{1}{x}) & if $x \neq 0$\ 0 & else}$ is differentiable everywhere. (NOTE: The first function is not differentiable, but the second is :) )
– Autho Jun 24 '19 at 19:52 -
^^ Note that $\cases{sin(\frac{1}{x}) & if $x \neq 0$\ 0 & else}$ is not even continuous!! – Autho Jun 24 '19 at 19:59
2
For $x\approx 0$, $$ x^n=o(x) \text{ and } 0=o(x) $$ so $$ \max\{0,x^n\}=o(x) $$ and hence the derivative is $0$ at $0$. At $x_0\neq0$ we get either $x^n$ locally, or $0$ locally, so differentiable.
user10354138
- 33,239
-
Thanks for answering. What is the definition of $o(x)$? Could you please explain a little more the equalities? – Thoth Jun 24 '19 at 19:06
-
It is the asymptotic little-o, i.e., $f(x)=o(g(x))$ if and only if $\lvert f(x)/g(x)\rvert\to 0$ as $x\to 0$. – user10354138 Jun 24 '19 at 19:14
2
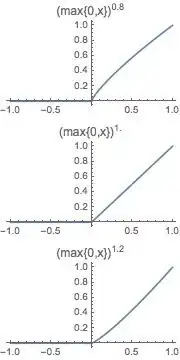
The slope of your function is zero on $(-\infty,0)$ (see the image below). For it to be differentiable at zero, its slope has to be zero on the right side as well. Your function restricted to $(0,\infty)$ is given by $x^n$. All you need is to show that the slope of $x^n$ at zero is zero for $n>1$.
stochastic
- 2,560
1
By the same argument as in the other post, on the right
$$f'(x^+)=nx^{n-1}$$ is zero at $x=0$ whenever $n>1$.