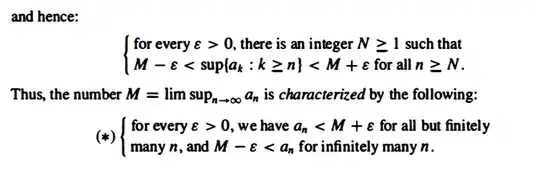1

For all $\epsilon > 0$, we have $a_n < M + \epsilon$ for all but finitely many $n$ and $M - \epsilon < a_n$ for infinitely many $n$. where $M = \limsup a_n$ (Carother page 12)

enter image description here

I am mainly having trouble with the second inequality $a_n > M - \epsilon.$ But I'll show you the first one anyways.

Let $(a_n)$ be a bounded sequence and $a_N^+ = \sup \{a_n: n \geq N\}$

By definition of $\lim$ we have

For all $\epsilon >0$, there is a integer $b$ such that $ \forall N \geq b \implies -\epsilon + M < a_N^+ < M + \epsilon.$

For the first part $a_N^+ < M + \epsilon$ is true for all $N \geq b$. Therefore by definition of sup, we have $a_n < M + \epsilon$ for all $n \geq b $. But it may not be true for $\{0,\dots, b\}$ of $b$ elements.

Now the thing that is throwing me off about the second one is that it mentions only infinitely many $n$.

For the inequality $M - \epsilon < a_N^+$ for $N \geq b$, by definition of supremum, there must be a point $c \geq b$ such that $n \geq c \implies M - \epsilon < a_n$.

But I do't see why we are withdrawing the "but finitely many" part for the other inequality.

Community
  • 1
Lemon
  • 12,664

2 Answers2

1

I can certainly explain the necessity of the second inequality, and why attaching an "all but finitely many" would make the characterisation too strong.

Consider the sequence $a_n = (-1)^n$. It's not hard to see that the limsup is $1$. It is not true, however, given any $\varepsilon > 0$, that for all but finitely many $n$, $a_n > 1 - \varepsilon$. In particular, if we take $\varepsilon = 1$ (or any $\varepsilon < 2$), then $$a_n > 1 - \varepsilon \iff 1 - a_n = 1 - (-1)^n < \varepsilon < 2 \iff a_n = 1.$$ There are, of course, infinitely many such numbers $n$ that fail to satisfy this condition: the odd numbers.

In fact, if it were true that $a_n > M - \varepsilon$ for all but finitely many $n$ and $a_n < M + \varepsilon$ for all but finitely many $n$, then both conditions would hold true for all but finitely many $n$, which is to say $$M - \varepsilon < a_n < M + \varepsilon \iff |a_n - M| < \varepsilon,$$ which means $M$ would have to be the limit of $a_n$.

So how do we prove this? Well, let's suppose $\varepsilon > 0$ and we have $N$ such that $$n \ge N \implies M - \varepsilon < \sup \{a_k : k \ge n \} < M + \varepsilon.$$ Assume $n \ge N$. Since $M - \varepsilon < \sup \{a_k : k \ge n \}$, it follows that $M - \varepsilon$ is not an upper bound of $\{a_k : k \ge n \}$. In particular, there must exist some $k_n$ such that $k_n \ge n$ and $a_{k_n} > M - \varepsilon$.

That's more or less it! There is one thing that we do have to mention: there are infinitely many $k_n$s. This has to be true, as $k_n \ge n$ for all $n \ge N$. So, there are infinitely many points in the sequence greater than $M - \varepsilon$.

Theo Bendit
  • 50,900
  • Sorry the question about "for all but finitely many", I probably meant to attach that to $\sup$ and that just happen to pass down to $a_n < M + \epsilon$. But it doesn't matter. For your proof regarding my second question. I am just comparing our indices here, are we writing the same thing? Also in my symbols, I really just thought $[c,\infty)$ was the infinite set they so talk about. – Lemon Jun 24 '19 at 07:39
  • No, I don't think we are writing the same thing. I'm saying, there exists an $k_n \ge n$ such that $a_{k_n} > M - \varepsilon$, whereas you seem to be saying there exists some $k_n$ (or $c$, in your notation) such that for all $m \ge k_n$, we have $a_m > M - \varepsilon$. This is much stronger, and much more false. – Theo Bendit Jun 24 '19 at 07:45
1

If $\epsilon>0$ and $M-\epsilon<a_n$ is only true a finite number of indices $n$ then there will be an index $N$ that satisfies: $$n\geq N\implies a_n\leq M-\epsilon$$

or equivalently:$$\sup\{a_n\mid n\geq N\}\leq M-\epsilon$$ Then however: $$M=\limsup a_n\leq M-\epsilon$$ which is absurd.

drhab
  • 151,093