$ \text{ Find } \lim_{n\rightarrow \infty} \frac{n}{a^n} $

Question

$\text{Find }$ $$ \\ \lim_{n\rightarrow \infty} \frac{n}{a^n} \\ \text{ where a > 0 is a number.} $$

$\text{To solve this problem we first realize that we need to use l'hopitals rule} \\ \text{because if we evaluate at infinity we get } \\ $

$$\lim_{n\rightarrow \infty} \frac{n}{a^n} = \frac{\infty}{\infty} \\ \text{using l'hopitals rule we get } \\ \lim_{n \rightarrow \infty}\frac{1}{n \cdot x^{n-1}} = 0 \\ \text{If we take lhopitals rule again we get } \\ \lim_{n \rightarrow \infty} \frac{0}{(n-1) \cdot n \cdot x^{n-2}} =0 \\ \text{Thus } \ \ \lim_{n\rightarrow \infty} \frac{n}{a^n} = 0 \\ \text{Is this the correct procedure that one uses in order to find the limit for this problem?} \\ \text{Is there any mistakes in my solution?} $$

The function does not always satisfy L'Hopital's hypothesis. — , Jun 22 '19 at 23:30
And, as it's been correctly pointed out, $\frac{d}{dx}[a^x]\ne xa^{x-1}$. — , Jun 22 '19 at 23:31
Related: https://math.stackexchange.com/questions/55468/how-to-prove-that-exponential-grows-faster-than-polynomial. And please, only use MathJax for the formulas, not for all the text... — Hans Lundmark, Jun 23 '19 at 07:26

Naji · Answer 1 · 2019-06-22T23:36:59.480

3

You are not differentiating $a^n$ (with respect to $n$) correctly.

$$ \frac{d}{dn}\left[a^n\right] = \text{ln}(a)a^n $$

So using L'Hopital's Rule (first time) you should get

$$ \frac{1}{\text{ln}(a)a^n} $$

Also note that if $0<a\leq 1$, then you will not be able to use L'hopital's Rule as

$$ \lim_{n\rightarrow\infty}\left[ \frac{n}{a^n}\right]=\frac{\infty}{0} $$

for $0<a<1$, and

$$ \lim_{n\rightarrow\infty}\left[ \frac{n}{a^n}\right]=\frac{\infty}{1} $$

for $a = 1$.

edited Jun 22 '19 at 23:36

answered Jun 22 '19 at 23:29

Naji

433

Is the limit then 0? – Jon Jun 22 '19 at 23:34
Depends on the value of $a$, will it converge for $a=\frac{1}{2}$? – Naji Jun 22 '19 at 23:40
It is 0 and $\infty $ that the limit can be depending on a. – Jon Jun 22 '19 at 23:52
Correct, you've proven the former with L'Hopital's rule - now you have to prove the latter, which is quite easy (Hint: $n\leq \frac{n}{a^n}$ if $a\leq 1$) – Naji Jun 22 '19 at 23:56

score 2 · Answer 2 · answered Jun 22 '19 at 23:31

For $a \leq 1$ the denominator does not tend to $\infty$ so L'Hopital's Rule is not applicable. For $a>1$ one application of the rule gives $\lim \frac 1 {a^{n}\log\, a}$ and $a^{n}\log\, a \to \infty$ so there is no need to apply the rule again. For $a\leq 1$ the limit is $\infty$. Can you prove this?

score 1 · Answer 3 · 2019-06-22T23:44:23.043

1

By L'Hôpital's rule, we get $\lim_{n\to\infty}\dfrac1{\ln a \cdot a^n}=0$, when $a\gt1$.

When $a\le1$, L'Hôpital isn't applicable. But the limit is easy to calculate. We get $\infty $.

edited Jun 22 '19 at 23:44

answered Jun 22 '19 at 23:34

Right @SaucyO'Path. I will try to clean it up. – Jun 22 '19 at 23:37
So this limit can have two solutions correct depending on a? – Jon Jun 22 '19 at 23:45
That's right, Jon. – Jun 22 '19 at 23:46
But after l'hopitals rule the limit can only be 0, so the limit is 0. – Jon Jun 23 '19 at 00:32
1

Yes. When $a\gt1$. – Jun 23 '19 at 00:33
Since when $a \le 1$ $lim_{n\rightarrow \infty} \frac{1}{a^n \cdot ln(a)} = \frac{1}{0} =\text{ Does not Exist}.$ – Jon Jun 23 '19 at 00:36
The numerator, $n$, goes to $\infty $. No L'Hôpital's rule when $a\le1$. – Jun 23 '19 at 00:47

score 1 · Accepted Answer · answered Jun 23 '19 at 00:37

L'Hospital's rule is only applicable when you have a limit of the form

$$\frac{\infty}{\infty}$$

or

$$\frac{0}{0}$$

Thus we need to consider $3$ cases: (a) $0<a<1$, (b) $a=1$, and (c) $a>1$.

(a) For $a<1$ we have

$$\lim_{n\to\infty}\frac{n}{a^n}=\infty$$

because $\lim_{n\to\infty}a^n=0$ and $\lim_{n\to\infty}n=\infty$, so we have

$$\frac{\infty}{0}=\infty, \quad 0<a<1$$

(b) When $a=1$, we have

$$\lim_{n\to\infty}\frac{n}{a^n}=\lim_{n\to\infty}\frac{n}{1^n}=\lim_{n\to\infty}n=\infty, \quad a=1$$

(c) For $a>1$ we have

$$\lim_{n\to\infty}\frac{n}{a^n}=\frac{\infty}{\infty}$$

This is the only case where L'Hospital's rule is applicable. Here, write

$$\begin{align}\lim_{n\to\infty}\frac{n}{a^n}&=\lim_{n\to\infty}\frac{\text{d}}{\text{d}n}\left(\frac{n}{a^n}\right)\\ &=\lim_{n\to\infty}\frac{\text{d}}{\text{d}n}\left(\frac{n}{\exp(\ln(a^n))}\right)\\ &=\lim_{n\to\infty}\frac{\text{d}}{\text{d}n}\left(\frac{n}{\exp(n\ln(a))}\right)\\ &=\lim_{n\to\infty}\frac{\text{d}}{\text{d}n}\left(\frac{1}{\ln(a)\exp(n\ln(a))}\right)\\ &=\lim_{n\to\infty}\frac{\text{d}}{\text{d}n}\left(\frac{1}{\ln(a)a^n}\right)\\ &=\frac{1}{\infty}\\ \lim_{n\to\infty}\frac{n}{a^n}&=0, \quad a>1 \end{align}$$

I added extra steps to demonstrate how to perform the derivative of $a^n$.

So we only use lhopitals rule once because, we get a form that is not $\frac{0}{0} , \frac{\infty}{ \infty}?$ — Jon, Jun 23 '19 at 00:55
@Jon correct. Consider $\lim_{n\to\infty}n$. The limit is clearly infinity. However, if we tried to apply L'Hospital's rule here, the limit would be come $\lim_{n\to\infty}1$, which is just $1$. L'Hospital's rule is only valid when we have one of those two forms, because in those cases, it is unclear what the answer is. Put another way, we do not apply L'Hospital's rule when we are already able to evaluate the limit. In those two cases, it is unclear if the denominator or numerator becomes smaller / larger faster, and L'Hospital's rule helps us to determine which one is. — Kraigolas, Jun 23 '19 at 01:17
Pardon me for asking but then case (c) would be the true limit solution posed by the original question. — Jon, Jun 23 '19 at 01:30
@jon because $a>0$, (a), (b), and (c) together define the solution to the problem. — Kraigolas, Jun 23 '19 at 13:18

scoopfaze · Answer 5 · 2020-02-19T07:07:53.927

Most of the answers provided seem to be tackle the problem by applying l'Hopital's Rule, which is a perfectly valid method. However, it's important to have an intuition for the limits you're solving. Since this is a fairly simple one, I'll use the opportunity to explain how to think about them.

With these types of questions, it's important to think about the growth rates of the functions you're comparing. In this case, the two you're comparing a linear function, $y=n$, to an exponential one, $y=a^n$. First, we can look at the numerator, which fairly clearly goes to $\infty$ in a linear fashion. As the other answers suggested, the exponential function requires looking at three cases, $a<1$, $a=1$, and $a>1$. The second of these intuitively goes to $\infty$, as:

$$\lim_{n\rightarrow\infty}\frac{n}{1^n}=\lim_{n\rightarrow\infty}n=\infty$$

For the case where $a<1$, hopefully it is clear that, the more times you multiply $a$ by itself, the smaller it becomes. Hence, when your numerator is going to infinity and your denominator approaches $0$, this is an indication that your limit also goes to $\infty$.

When $a>1$, now you should consider how the two different functions grow. Looking at the case when $a=2$, we have this graph:

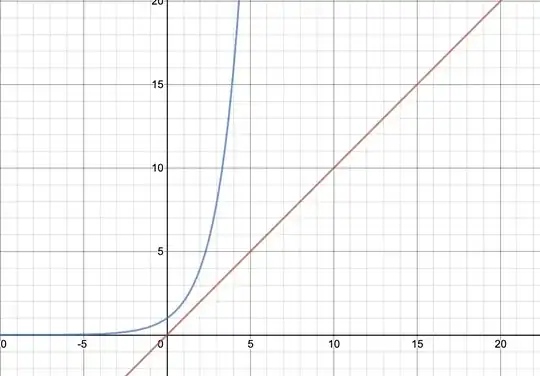
where the red graph is the line $y=x$ and the blue graph is $y=2^x$. Through graphing, you can clearly see the trends that the two functions have when increasing, and you can deduce that $y=2^x$ will "get to" $\infty$ "faster" than $y=x$ will. It's this kind of thinking that underlies the problem: which of these two functions that I'm comparing will reach infinity faster? If the one in the denominator does, then you should gain the intuition that your limit may go to $0$ (and $\infty$ if the numerator approaches it faster). There's nothing wrong with l'Hopital's Rule for more grueling limits where it's harder to have a feel about the problem, but I think it's important to have a conceptual grasp on how to think about these problems before you automatically apply it.

$ \text{ Find } \lim_{n\rightarrow \infty} \frac{n}{a^n} $

5 Answers5