Related to An ancient Japanese geometry problem
As illustrated in the other question, one branch of the solution to the equation
\begin{align} 16\,t^5 -8\,c (5\,c +2) t^4 +c^2 (25\,c^2+20\,c + 36) t^3& \\ -4\,c (11\,c^3+8\,c^2+5\,c+2) t^2& +8\,c^2 ( 3\,c^2+3\,c+2 ) t -4\,c^3 (c+2) =0 \tag{1}\label{1} \end{align} (which is quintic in $t$ and quartic in $c$) corresponds to a valid partitioning (with the three congruent incircles) of the isosceles triangle with the unit legs and the base $c$.
So it would be nice to have the representation of this branch in a form of some sort of a function $f:c\to t$ in order to be able to make a proper construction easily, since the process of solving quintic equations in known to be messy.
Luckily, it is possible to find much more "exact" points on that curve: feeding \eqref{1} with some rational value of $t$, we get a quartic in $c$, which, surprisingly, mostly results in more-or-less "digestible" expressions in terms of square roots. For example, the exact value of $t=\tfrac35=0.6$ corresponds to $c=-5+\tfrac45\sqrt{85}-\tfrac15\sqrt{2075-218\sqrt{85}}\approx 0.761457$.
Unfortunately, the bigger integers are used in the rational $t$, the bigger numbers appear in the expression for $c$, so at some point it becomes unpractical.
On the other hand, feeding the value of $c$ into \eqref{1} looks to be less fruitful, it mostly results in an unsolvable quintic. Even the equilateral case, when $c=1$, results in
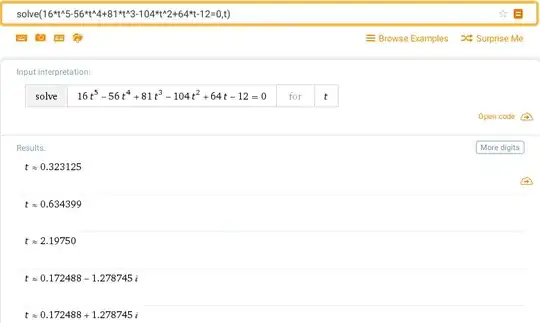
\begin{align} 16t^5-56t^4+81t^3-104t^2+64t-12&=0 , \end{align} for which the Wolfram Alpha gives only numeric output with the three real roots:
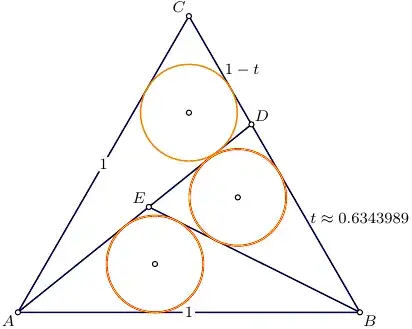
In this case the correct root is $t\approx 0.6343989078979$ and the corresponding picture is
Also, an interesting case corresponds to the end point of the branch, a "collapsed" triangle with $c=2$. In this case the quintic factors out
\begin{align} 16t^5-192t^4+704t^3-1056t^2+640t-128 &= 16(t^3-8t^2+8t-2)(t-2)^2 \end{align} and we have a closed-form expression
\begin{align} t&=\tfrac83-\tfrac23\sqrt{10} \cos(\tfrac13\arctan(\tfrac 3{251}\sqrt{111})) +\tfrac23\sqrt{30}\sin(\tfrac13\arctan(\tfrac3{251}\sqrt{111})) \\ &\approx 0.71274226238 . \end{align}
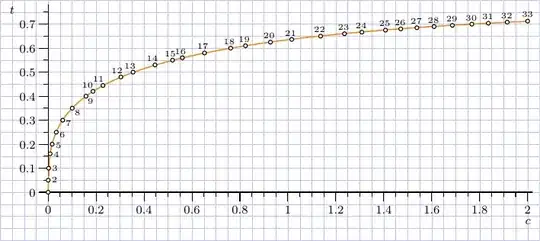
For the reference, this is the list of all "exact" pairs $(c,t)$:
$$ \begin{array}{c|c|c|} & c & t \\ \hline 1&0.0000000000&0.0000000000 \\ 2&0.0002511171&0.0500000000 \\ 3&0.0020326859&0.1000000000 \\ 4&0.0085083955&0.1600000000 \\ 5&0.0169302697&0.2000000000 \\ 6&0.0340089030&0.2500000000 \\ 7&0.0608062789&0.3000000000 \\ 8&0.1006330785&0.3500000000 \\ 9&0.1579689782&0.4000000000 \\ 10&0.1871535034&0.4200000000 \\ 11&0.2287638337&0.4444444444 \\ 12&0.3033618942&0.4800000000 \\ 13&0.3542486889&0.5000000000 \\ 14&0.4456874846&0.5300000000 \\ 15&0.5189509162&0.5500000000 \\ 16&0.5600000000&0.5600000000 \\ 17&0.6524875367&0.5800000000 \\ 18&0.7614570341&0.6000000000 \\ 19&0.8233447531&0.6100000000 \\ 20&0.9271847561&0.6250000000 \\ 21&1.0160639236&0.6363636364 \\ 22&1.1365368495&0.6500000000 \\ 23&1.2361295561&0.6600000000 \\ 24&1.3086349633&0.6666666667 \\ 25&1.4070647569&0.6750000000 \\ 26&1.4707414304&0.6800000000 \\ 27&1.5382434439&0.6850000000 \\ 28&1.6099068664&0.6900000000 \\ 29&1.6861084399&0.6950000000 \\ 30&1.7672719250&0.7000000000 \\ 31&1.8360946829&0.7040000000 \\ 32&1.9148985973&0.7083333333 \\ 33&2.0000000000&0.7127422624 \\ \hline \end{array} $$
so it was possible to find an approximation of the form \begin{align} t\approx f_a(c)&=a_0\,c^{a_1}-a_2\,c^{a_3} ,\\ \text{where}\quad a_0&=0.8607785404155162 ,\\ a_1&=0.3444908412558547 ,\\ a_2&=0.22578038518570656 ,\\ a_3&=0.7556569650006819 . \end{align}
This approximation works surprisingly well - the maximal deviation of the mentioned interpolation points is about $0.001$, which would be unnoticed in the illustrative drawings.
At least this approximation can be used to feed an initial value to the numerical root-finding methods using, for example, Halley’s root-finding algorithm to get more accurate result.
Question: Any suggestions on the better/simpler approximating function (not piecewise interpolation)?