0

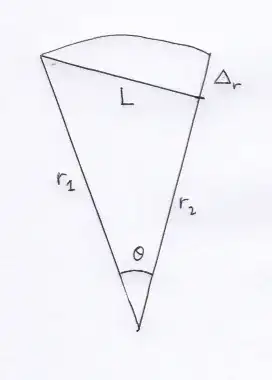
I have to place a series of line segments along an $r=k\theta$ spiral. All the line segments are the same length (which I will call $L$) and the starting point of each is the finish point of the previous.

For my task I decided it will be easiest to do if I can determine the next radius $r_2$ from the previous radius $r_1$ (or the angle $\theta$ from the previous radius $r_1$).

$ \hskip 2.0 in$enter image description here

So, I have the equations:

$r_2 = r_1 - \Delta r$

$\Delta r = k \theta$

and of course all the triangle relations from $\theta$ being between $r_1$ and $r_2$ and opposite $L$.

I plugged them together to get $r_1-k \theta=r_1\cos(\theta)\pm\sqrt{L^2-r_1^2\sin^2(\theta)}$

So, I need to solve for $\theta$ to get my $\theta$ and $r_2$. But, I don't know how to do this and the online solvers can't manage it (although they can solve very close ones...) Can anyone help with it?

Thank you!

xrfxlp
  • 1,505
user183966
  • 103

1 Answers1

1

It might be easiest simply to do it numerically -- write a parametric equation for your spiral and use bisection (or possibly Newton-Raphson) to find the parameter for the next point that has the desired distance from your current one.

hmakholm left over Monica
  • 286,031
  • Thank you Henning. I would love to write a little script to do it, but unfortunately I have to plug it into my CAD program so it would be ideal if I could get a closed form solution. Or even an approximate algebraic solution. – user183966 Jun 18 '19 at 16:22
  • @user183966: I think you're out of luck for a closed-form solution. The law of cosines gives something only slightly nicer than your equation -- there's no square root, but still a mixed second-degee equation in both $\theta$ and $\cos\theta$. Since even $x=\cos x$ doesn't have a nice closed solution, this looks like a place where a wise man ought to cut his losses. – hmakholm left over Monica Jun 18 '19 at 16:44
  • Ok, thank you very much. Maybe I will make some kind of horrible excel sheet and import the numbers then! – user183966 Jun 18 '19 at 16:55