Graphing $x^{2/3}$: a question of domain

Question

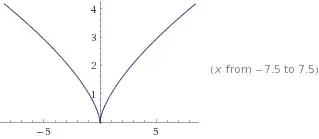
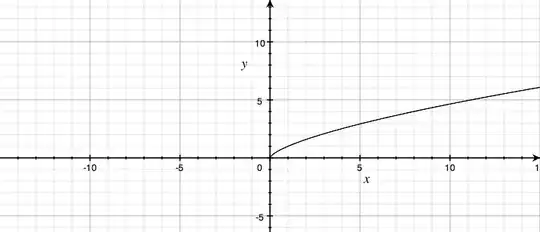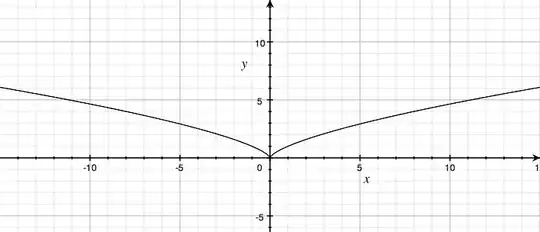
I'm trying to graph $x^{2/3}$. If I enter $y=x^{2/3}$, my graphing program excludes negatives from the domain: x to the two-thirds However, if I enter it as either $y=\sqrt[3]{x^2}$ or $y=(x^{1/3})^2$, it includes the negative values of $x$: cube root of x-squared

I'd like to understand what's going on. My best guess is that while $x^{2/3}$ is well defined for negative values of $x$ (since the fractional exponent's denominator is an odd integer), the graphing program is being overly cautious in interpreting the expression. But that's just a guess. Any ideas what's happening here?

Thanks for the responses. As it seems this is a duplicate of a previously posted question, I'll vote to close this.

I can't find it, but there was an earlier post with this exact problem: graphing $x^{2/3}$, with the same outcomes, depending on the way the function was keyed in, as in your case. So it's a hardware/software "thing" with the calculator. I think it was a TI-83+/84+/titanium (can't remember that). The post showed the same graphs for the same input. I can picture the post now! — amWhy, Mar 10 '13 at 16:16
This boils down to: Never trust your pocket calculator (or other software) to use exactly the definition of a function that you have in mind. — Hagen von Eitzen, Mar 10 '13 at 16:19
possible duplicate of How do you compute negative numbers to fractional powers? — , Mar 10 '13 at 16:50

score 5 · Answer 1 · answered Mar 10 '13 at 15:14

5

It likely comes down to the fact that your graphing program is using an approximation for $2/3,$ and said approximation has an even denominator.

answered Mar 10 '13 at 15:14

Cameron Buie

102,994

I would think if that were the case it would do the same for 1/3, but it doesn't ($x^{1/3}$ handles the negatives no problem). You could be right though. – ivan Mar 10 '13 at 16:09

score 2 · Accepted Answer · edited Apr 13 '17 at 12:21

2

The issue is that there are three sorts of things one could mean when one writes down an exponentiation, and the differences between them become quite significant when you consider negative bases.

Here is an answer I've written to another question talking about a similar question.

edited Apr 13 '17 at 12:21

Community

1

answered Mar 10 '13 at 16:53

score 1 · Answer 3 · answered Mar 10 '13 at 16:22

1

Can't post this as a comment, but note:

WolframAlpha: $y = x^{2/3}$:

enter image description here

WolframAlpha: $y = \sqrt[3]{x^2}$:

enter image description here

Note: the scales for graphing are different, but there is clearly a difference with respect to how Wolfram interprets each of the inputs. And the first plot adds an additional anomaly.

answered Mar 10 '13 at 16:22

amWhy

209,954

That 1st plot is trying to show 3D of data in just 2D. The imaginary part (x<0) should be added to the real part to produce a curve in [x,y,z] space. – amI Oct 17 '16 at 21:17

score 1 · Answer 4 · edited Mar 10 '13 at 16:58

1

Here is the reason I think Softwares interpret both expressions in a different way

$$ x^{\frac{2}{3}} = \exp\left ( \frac{2}{3} \ln \left ( x \right ) \right ) $$ Works only if $x>0$

$$ \sqrt[3]{x^{2}} = \exp\left ( \frac{1}{3} \ln \left ( x^{2} \right ) \right ) $$ Works whatever $x$ value

edited Mar 10 '13 at 16:58

Américo Tavares

38,602

answered Mar 10 '13 at 16:41

Gabriel Romon

35,428
5
65
157

Graphing $x^{2/3}$: a question of domain

4 Answers4