1

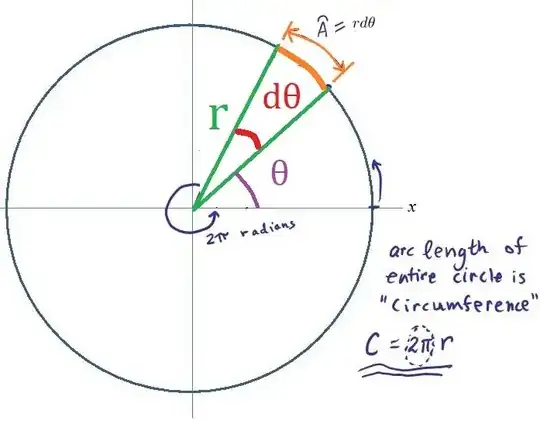
As in this post, I'm trying to understand why area of a sector of a circle $= \dfrac{\theta r^2}{2} $ WITHOUT relying on $\dfrac{\theta }{2\pi} \pi {r}^{2}$ or $\dfrac{\theta }{2\pi} 2 \pi {r}$ or integrals. To picture the emboldened phrase in Skeeter's reply, I edited this picture, but I can't picture why the orange curve is $r⋅dθ$?

enter image description here

to justify this formula w/o using the mentioned geometrical relationship requires the use of the calculus ...

consider a sector with a very small $θ=dθ$, and note the area of a small sector is close to the area of a triangle.

remembering the area of a triangle, $A=bh/2$ , the base is the small arclength equal to $r \cdot dθ$ and the height is equal to $r$ ...

a small sector of the large sector has area $dA=\dfrac{bh}2=\dfrac{r⋅dθ⋅r}2=\dfrac{r^2⋅dθ}2$

suffice it to say that summing all the small sectors that make up the larger sector results in $A=\dfrac{r^2⋅θ}2$

Community
  • 1

3 Answers3

2

If the angle measure is $d\theta$, then the arc is $r\,d\theta$. That's from the definition of radians. In other words, the angle measure unit of radians is chosen specifically so that this works.

Arthur
  • 199,419
1

You ask for this not to rely on $\frac{\theta }{2\pi} \pi {r}^{2}$ (proportion of the circle area), but you do not mention $\frac{\theta }{2\pi} 2\pi r$ (proportion of the circle circumference) as a prohibited step.

So you could think of it as saying:

  • The circumference of a circle is $2\pi r$
  • The angle you are interested in is $d\theta$
  • That angle is a proportion $\frac{d\theta}{2\pi}$ of the total angle of the circle
  • Since a circle has circular symmetry, the arc length you are interested in is $\frac{d\theta}{2\pi}2\pi r = d\theta\, r$
Henry
  • 157,058
  • I did mean to forbid this step too, and I added it to my answer. Can you please change your answer? –  Jun 20 '19 at 09:01
  • 1
    @Amandad'Halluin The problem is that you have excluded everything that enables $\theta$ of $d\theta$ to be defined. I used a unit circle having a full angle of $2\pi$, but you have forbidden that. Note that if a full circle had an angle of $360^\circ$ then the arc length is not $r , d\theta$ but $r \frac{2 \pi , d\theta}{360}$ – Henry Jun 20 '19 at 13:16
1

As I mentioned in another post here:

https://math.stackexchange.com/a/3231322/11172

there really isn't any way to deal with this kind of thing "without integrals". The problem is that in order to make sense of the arc length and/or area at all, you have to use some kind of calculus, i.e. a limiting process. This was understood all the way back to the time of Archimedes, who considered the problem by inscribing and circumscribing regular polygons inside and outside the circle as bounds, with larger and larger numbers of sides to estimate the perimeter and area, and show the area is proportional to the square of the radius (if I remember right).

Note that appealing to the "definition of radians" is not really an answer, because the definition of radians references arc length - it would thus be circular (pardon the apparent pun) reasoning if you don't have an independent, free-standing definition of arc length to begin with.

Insofar as to why any such definition must involve some form of calculus, it's because $\pi$ is a transcendental number. No solution of purely algebraic equations (that don't reference other transcendental numbers) will yield such numbers, effectively by definition. Alternatively, if you are given a field of numbers that are constructible using more "elementary" methods, e.g. the rationals, or the Pythagorean numbers (numbers that can be built using a compass and straightedge a la Euclid), or the algebraic numbers, you can only get to the generic reals by effectively taking limits: in fact, you can consider the ability to take limits, i.e. to do calculus, to be the crucial trait that defines the reals, in a sense which can be made precise in more than one way. And $\pi$ has to come out of the process somehow.

The_Sympathizer
  • 19,651