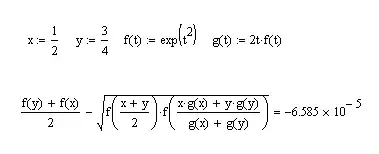New bounds for convex function of 2 variables

Question

It's related to my post : New bound for Am-Gm of 2 variables

In fact I have discovered (maybe it's already knew) a new formula for convex function this is the following :

Let $f(x)$ be a twice differentiable function on an interval $I$ with :

1) $f(x)\geq 0\quad \forall x \in I$

2)$f''(x)\geq 0\quad \forall x \in I$

3)$f(x)\neq \text{constant function} $

Then we have for $x,y \in I$: $$\sqrt{f\Big(\frac{xf'(x)+yf'(y)}{f'(x)+f'(y)}\Big)f\Big(\frac{x+y}{2}\Big)}\leq \frac{f(x)+f(y)}{2}\leq \frac{f\Big(\frac{xf'(x)+yf'(y)}{f'(x)+f'(y)}\Big)+f\Big(\frac{x+y}{2}\Big)}{2}$$

For the RHS we can use Karamata's inequality , the first line of the majorization is easy to check the second line gives :

$$x+y\leq \frac{xf'(x)+yf'(y)}{f'(x)+f'(y)}+\frac{x+y}{2}$$

Or after manipulation:

$$\frac{x+y}{2}(f'(x)+f'(y))\leq xf'(x)+yf'(y)$$

Wich is true because $f'(x)$ is increasing ($f''(x)\geq 0$) .

The LHS is more delicate and it's the reason why I post here . Maybe we can introduce the logarithm and see what happend...

So if you have any hints it would be nice (or a counter-example) .

Thanks in advance for your time .

Ps: For the story I'm inspired by Slater's inequality and Jensen's inequality .

Answer 1

The left hand side of the inequality fails for $f(x)=e^{x^2}$, $x=0$, $y=1$ , and $I=[x,y]$. Indeed, $f’(t)=2te^{t^2}$ for each real $t$. So $f’(x)=0$ and the left hand side of the inequality transforms to a false inequality $\sqrt{f(1)f\left(\frac 12\right)}\le \frac {1+f(1)}2$ or $\sqrt{e\cdot e^{1/4}}=1.868\dots \le 1.859\dots=\frac {1+e}2$.

The inequality also fails for $x=\tfrac 12$ and $y=\tfrac 34$, see the following Mathcad calculations.

Answer 2

In a comment to another question by FatsWallers, Paata Ivanishvili pointed out that the right inequality is wrong too. In fact, it is false for $f(x)=x^3+ax$ for every positive $a$ and $I=[0,\sqrt{a}]$. Setting $x=\sqrt{a}/3$, $y=2\sqrt{a}/3$, the RHS minus the LHS is $-19/31944\cdot\sqrt{a^3}<0$.