10

Thanks for reading.

THE QUESTION:

Convince me that when on the surface of a smooth hill, the $(x,y)$ direction I should take a tiny step in such that my current height doesn't change is always perpendicular to the $(x,y)$ direction I should take a tiny step in so that my height changes by the most.

More Mathematically formulated:

Convince me, intuitively, that the direction of steepest ascent is perpendicular to the level-set of a function.

Convince me, intuitively, that if I"m standing on a smooth hill, the direction of steepest ascent is perpendicular to the direction I should move in so that the height doesn't change at all.

Why I'm asking it:

(This section is going to be really long, but just because I want to be helpful to potential responders and explain exactly what I understand and what I don't understand in as much depth as possible. If you read it all, thank you so much!)

I've always had trouble understanding that the gradient is the direction of steepest ascent.

I've seen some excellent answers on this site, like this one...

Why is gradient the direction of steepest ascent?

...and this one...

Gradient of a function as the direction of steepest ascent/descent

...and honestly, most answers seem to answer in the same way: by proving that the dot product of a vector of fixed length with the gradient, which by definition is the change in the function at that point, is maximum when the vector of fixed length (the step) points in direction of the gradient.

That answer is fine...but I've always had a little bit of trouble understanding it.

That's because although the phrase "...take the step that points in the direction of the gradient to maximize the dot product between the step's direction and the gradient..." is mathematically sound, the idea of "the direction" of the gradient isn't something I"m really comfortable with, since I view the gradient as an operator on a vector $\begin{bmatrix} dx\\ dy \end{bmatrix}$ that outputs by how much some $f(x,y)$ would change at some specific $(x,y)$ if we took that "step". It's hard for me to think of the gradient as a vector itself.

So yea, I've never really truly understood the "direction of steepest ascent" of a function.

However, something I DO understand is the level-sets of a function. These are all the $(x,y)$ points such that some $f(x,y)$ stays constant.

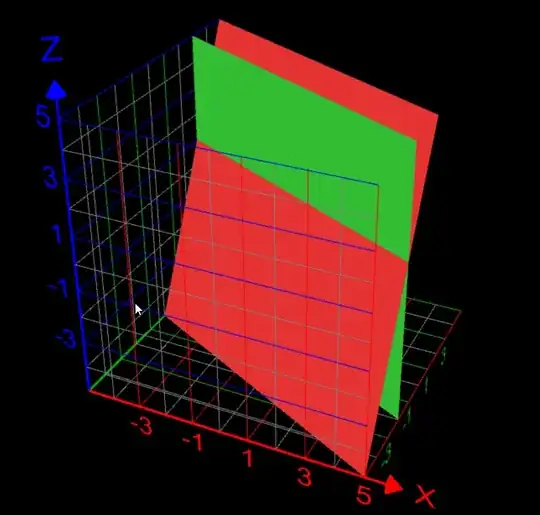
For example, if $f(x,y)=x+2y$, then $(x+2y)=1$ would be a level-set.

enter image description here

In the picture above, the red plane is $z=f(x,y)$, and the green plane is $(x+2y)=1$. As you can see, the intersection of the two planes is flat, indicating that $f(x,y)$ is constant for all $(x,y)$ such that $(x+2y)=1$.

Now, say I was standing on that intersection, where $z=1$, and I wanted to know which $(x,y)$ direction to take a step in so that I didn't move up or down the mountain?

I would need to move in a $(x,y)$ direction such that $(x+2y)$ stayed constant.

Say I take a tiny step in some arbitrary direction. That step will have an $x$ component and a $y$ component.

We can represent that tiny step as a vector: $\begin{bmatrix} dx\\ dy \end{bmatrix}$.

For whatever tiny amount $dx$ that step corresponds to in the $x$ direction, $f(x,y)$ (my height) will change by $dx$, since at that $(x,y,f(x,y))$ point I'm standing on on that smooth mountain, $\frac{\partial f}{\partial x}=1$.

On the other hand, for whatever tiny amount $dy$ that step corresponds to in the $y$ direction, $f(x,y)$ (my height) will change by $2dy$, since at that $(x,y,f(x,y))$ point I'm standing on on that smooth mountain, $\frac{\partial f}{\partial y}=2$.

In general, at any $(x,y,f(x,y))$, the amount by which $f(x,y)$ changes when I take a tiny step $\begin{bmatrix} dx\\ dy \end{bmatrix}$ is the amount by which it changes due to the component of our step in the $x$ direction, which would be $\frac{\partial f}{\partial x} * dx$, plus the amount that it changes in due to the component of our step in the $y$ direction, which would be $\frac{\partial f}{\partial x} * dy$.

In this specific example, the function changes twice as much for any step in the $y$ direction than it does for any step in the $x$ direction. That means that if I don't want $f(x,y)$ to change at all, then for whatever amount I move in the $y$ direction, I must move negative twice that amount in the $x$ direction, since any fixed amount of movement in the $y$ direction corresponds to twice the change in height as does any movement in the $x$ direction!

In other words, the direction of my step should be: $\begin{bmatrix} -2\\ 1 \end{bmatrix}$.

Let's say I was instead standing at an $(x,y,f(x,y))$ point where a tiny step in the $x$ direction corresponded to 42 times the change in altitude than a tiny step in the $y$ direction did.

In other words, $\frac{\partial f}{\partial x}=42\frac{\partial f}{\partial y}$ at that point.

Then, to not change height at all (stay on the level-set), I would want to take a tiny step in the $\begin{bmatrix} 1\\ -42 \end{bmatrix}$. I'd want to make sure that my step moves me $-42$ times as much in the $y$ direction as we do in the $x$.

More generally, if I'm standing at some point $(x,y,f(x,y))$ on a smooth mountain, the step I should take such that my altitude doesn't change (such that $f(x,y)$ doesn't change) should always be $\begin{bmatrix} +\frac{\partial f}{\partial y}\\ -\frac{\partial f}{\partial x} \end{bmatrix}$

This makes sense to me - no dot products needed so far!!!!

Now, I know that the direction orthogonal to $\begin{bmatrix} +\frac{\partial f}{\partial y}\\ -\frac{\partial f}{\partial x} \end{bmatrix}$ corresponds to taking the negative reciprocal of it.

That is:

$\begin{bmatrix} \frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y} \end{bmatrix}$

AND THAT'S THE DIRECTION OF STEEPEST ASCENT!

In summary, I understand why the "direction of no ascent" is what it is.

If I could somehow intuitively understand that the "direction of steepest ascent" when climbing a mountain is always perpendicular to the direction of no ascent, then I would understand why the gradient is in the direction of steepest ascent.

Thanks!

One more thing...

I tagged this question as a soft question simply because I'm looking for intuitive answers more than mathematical proofs, and it's hard to say whether or not intuitive answers are correct.

Copied and pasted from a comment below...

I'd like to be able to picture myself standing on the surface of a smooth hill, standing over a spot where someone took a bright neon marker and traced out a level-curve on that hill, and picture the hill in such a way that the direction in which the hill is steepest is OBVIOUSLY perpendicular to that hill. And as of now, I just can't! It seems just as plausible that some OTHER direction not perpendicular to that bright yellow level-curve could be the steepest direction instead!

joshuaronis
  • 1,479
  • 10
  • 29
  • Good question. "the idea of 'the direction' of the gradient isn't something I'm really comfortable with, since I view the gradient as an operator on a vector..." I wonder if you're not being a bit stubborn in this viewpoint. The gradient operator takes a vector $v$ as input and computes the dot product of $v$ with a certain vector $g$. This vector $g$ is an important part of the picture, and it deserves to have a name and to be understood. The operator viewpoint doesn't mean we have to throw $g$ out the window. If you don't want to call it the "gradient", call it something else. – littleO Jun 11 '19 at 15:21
  • @littleO thanks for the input! And I agree completely with you. I understand that the gradient as an operator is, computationally, equivalent to taking the vector $\vec{g}$ and taking its dot product with $\vec{v}$. And I also understand that a dot product between two vectors is maximized when $\vec{v}$ and $\vec{g}$ point in the same direction. It's just that for me personally, since it's just so much easier to think of the "direction of no ascent" than the "direction of steepest ascent", if I understood it from this viewpoint I'd have a much better understanding of $\vec{g}$. – joshuaronis Jun 11 '19 at 15:38
  • And also, although it seems like it SHOULD make intuitive sense that the direction of steepest ascent is always perpendicular to the direction of no ascent, when I try to explain it to myself intuitively...I can't seem able to! And, "if I can't explain it simply, I don't understand it well enough" (one of those cheesy quotes, I think people say it was einstein). Thanks! – joshuaronis Jun 11 '19 at 15:40
  • 1
    Suppose you're located at $x$, and $u$ is a direction of no ascent at $x$. You move a bit, in a certain direction, hoping to increase the value of $f$ as much as possible. (I like to imagine I'm a mosquito looking for a warm spot in $\mathbb R^3$.) If your displacement vector $v$ has a nonzero component in the direction $u$, then that nonzero component is wasted motion. Any motion in the direction $u$ is not helpful. Instead of moving in the direction $v = cu + w$, you could have increased the temperature just as much (while moving a shorter distance) by just moving in the direction of $w$. – littleO Jun 11 '19 at 16:17
  • @littleO yep - that makes sense mathematically (and perhaps intuitively too to a lot of people). However, for some reason, I still can't make a visual connection. I'd like to literally be able to picture myself standing on the side of a hill, standing over a spot where someone took a bright neon marker and traced out a line of a level-curve on that hill, and picture the hill in such a way that the steepest direction is perpendicular to that hill. And as of now, I just can't! – joshuaronis Jun 11 '19 at 19:02
  • This question (at least, the one described in the title) can be answered without using the word "gradient" at all. But the kind of function of two variables that has level sets is a scalar function (two numbers as input, one number as output), and the gradient of such a function is a vector. Notationally, if the function is named $f: (\mathbb R\times\mathbb R)\to\mathbb R,$ and $(x,y)\in\mathbb R\times\mathbb R$, then $\nabla f(x,y)$ is a vector. http://fourier.eng.hmc.edu/e161/lectures/gradient/node3.html – David K Jun 17 '21 at 02:38
  • Does this answer your question? Why is gradient the direction of steepest ascent? – tryst with freedom Apr 27 '22 at 05:31

2 Answers2

5

I don't know how helpful this will be, it's just the way I sometimes like to picture it.

Since your hill is smooth, it's locally just a plane (more precisely, there exists a tangent plane which is an approximation that is at least quadratically good).

Now take this plane and cut out a small disk where you're standing (it will in general be slanted). Draw its horizontal diameter, which is (a piece of) a level set. If you grab the disk at the points where this diameter intersects the boundary and look at it head-on, being careful to only rotate it about the vertical axis, you may be able to convince yourself that indeed the only possibility is going perpendicular to the diameter.

This is rather vague, I hope it's not completely useless.

J_P
  • 2,148
  • That's perfect! Thanks! That's exactly the sorts of answers I'm looking for - little intuitive ways to think about it like that. Thank you! +1 – joshuaronis Jun 11 '19 at 15:43
  • What do you mean by "where the diameter intersects the boundary"? The boundary of the disk? – joshuaronis Jun 11 '19 at 15:45
  • Yes, like if you draw a diameter on a circle floating in 3D space; I'm talking about the two edge points of this line segment. – J_P Jun 11 '19 at 15:49
  • You can also not even use a disk and just visualise some piece of the plane, but I prefer a disk because it's a definite shape. – J_P Jun 11 '19 at 15:50
  • So pretty much what you're saying is: 1. Convince yourself that the direction of steepest ascent is perpendicular to the level-set for a plane. 2. Make a plane tangential to the smooth hill. 3. If the plane is tangential to the smooth hill, the direction of steepest ascent for the hill is equal to the direction of steepest ascent for the plane-QED. Hmm, I like it, but my biggest problem is that (and this is definitely my fault for not understanding tangency in dimensions greater than 2D yet) I can picture balancing the disk on a point on the surface of the hill and pivoting it... – joshuaronis Jun 11 '19 at 15:56
  • ...around so that it still only touches the hill at a single point, but the slope of steepest ascent of the disk changes. Maybe I should ask this as a separate question...but why would that not be possible? Why can't there be different orientations in which I could orient the disk and still only have it touch the 3D surface at a single point? It seems like there would...maybe I just have to try visualizing it for longer? – joshuaronis Jun 11 '19 at 15:57
  • You have to be careful to really imagine pivoting it around a point, not rolling it around on the surface. Anyway, strictly speaking, it's not so much about touching in a single point (for example the function $xy$ has a horizontal tangential plane at $0$ which intersects the graph in along two lines). It's more about being "the best" we can do with a linear thing (the plane). – J_P Jun 11 '19 at 16:20
  • 1
    Maybe you can do this: instead of dealing with the entire graph, take two perpendicular lines in the $xy$ plane, perhaps $x=const., y=const.$ Then slice the graph of your function along these two lines which gives you two spaghetti floating in 3d space. You have to "glue" a plane to their intersection as flatly as possible. If you look at the spaghetti really close, they're basically lines. Maybe this can help visualize why there's only one tangent plane. – J_P Jun 11 '19 at 16:23
  • Basically, once you have a tangent plane, any other tangent plane would have to be tangent to the surface but this would mean it's tangent to the original plane, so it's just the same plane. Though being honest, I can't quite visualize why there's only one such plane either. – J_P Jun 11 '19 at 16:24
  • 1
    Yeah, it's really not the right intuition that the tangent plane is a plane that just touched the hill in one point. Rather the tangent plane is the plane that is the same shape as the hill, up to trivial errors, when you zoom in close enough. That presentation makes it clear that there's only one tangent plane. – Kevin Carlson Jun 11 '19 at 16:30
  • @J_P I loved that spaghetti explanation, thank you so much! Is there some other place where the question is addressed, that is, the question of: "Why if the tangent plane agrees with the slope of the function in both the x and the y directions (both the spaghetti directions) it automatically agrees with the slope of the plane in every direction? Formally or intuitively? Should I just ask a separate question on SE? I'm still having a little trouble with it...like I feel that it SHOULD make sense, but...I can't put it into words why. – joshuaronis Jun 15 '19 at 21:54
  • @J_P I can see that if the spaghetti (perpendicular axes that we're placing the plane on) pointed in different directions, the tangent plane would change. But, what I can't see is why the fact that the plane gets put on those two "spaghettis", so its slope agrees with the slopes of the spaghettis, means that its slope also agrees with the slope of EVERY POSSIBLE spaghetti we could've cut out at that point in the curve...idk if that question makes sense lol. But I AM fascinated by the spaghetti explanation! – joshuaronis Jun 15 '19 at 22:07
  • 1
    It doesn't necessarily. This means that the partial derivatives exist but that the function is not differentiable. Actually, looking back at this, I think the way Kevin Carlson put it is clearest. For a function to be differentiable, this means that if you keep zooming in ad infinitum, if you're a tiny tiny speck on the graph, you won't even be able to perceive any curvature at all and the graph will look just like a plane. That plane that you "see" is the tangent plane. – J_P Jun 15 '19 at 22:08
  • If it is differentiable, then the spaghetti all lie flat on the plane. But I guess I'm getting kind of circular now. – J_P Jun 15 '19 at 22:12
  • Maybe it is really better not to begin with the spaghetti but the zooming-in tactic. I don't think I can come up with any undisputable visuals, though... – J_P Jun 15 '19 at 22:19
  • @J_P Wow, that's really weird that the function can be differentiable in two directions, but not in others...I'm trying to picture it, but I can't... Okay, and just one more question, since I know they discourage extended discussions on most of these stack exchange sites. Let's say that the function IS differentiable at that point. Can you come up with a way to convince me that then if the plane agrees with two spaghettis, it will agree with every direction (every possible spaghetti)? It doesn't have to be visual, but someone somewhere must've explained or proved why at some point! – joshuaronis Jun 16 '19 at 13:44
  • To be concise: if a function is differentiable at a point, and we fit a tangent plane to that point so that the slope of the tangent plane agrees with two possible directions at that point (the x and the y directions), why does it automatically agree with every possible direction? Additionally, an intuitive visual explanation would be nice, but so too would a proof, so that I can carry this on into higher dimensions. Thanks, and thanks for all the comments beforehand as well! – joshuaronis Jun 16 '19 at 13:47
  • There is one trivial example of such a function: $1$ on the coordinate axes and $0$ everywhere else. Then at $(0,0)$ the partial derivatives in $x,y$ clearly exist, but no other directional derivatives do. There are supposedly even stranger examples where the directional derivatives exist but still the function is not differentiable. – J_P Jun 16 '19 at 17:39
  • What you're asking about I think follows directly from the definition of differentiability, as found e.g. here https://en.wikipedia.org/wiki/Differentiable_function#Differentiability_in_higher_dimensions Once you have the linear operator $J$, restricting $h$ to lie along a certain direction (on a line) reduces to the definition of the directional derivative (I think), which should imply that the derivative is just $J(h)$, so $J$ applied to $h$. For $f(x,y)$, $J$ is in fact a dot product with some vector which is just the gradient, and this gives the familiar $\partial_s f=\nabla f\cdot s$ – J_P Jun 16 '19 at 17:55
  • $z=\nabla f\cdot (x,y)$ is also the equation of a plane and if you cut it along a line $s$ in the $xy$ plane you get a line in $3D$ space with slope in $z$ exactly $\nabla f\cdot s$, so this equals the inclination of that spaghetti, because that is just the directional derivative. I think to picture it is really just to zoom in until you can't possibly distinguish the graph from a plane anymore, and then for the plane obviously every line in the plane is tangent to the plane. If you want to discuss this further, I suggest you move it to chat. – J_P Jun 16 '19 at 18:03
  • Let us continue this discussion in chat. – J_P Jun 16 '19 at 20:24
4

An old question, but a good one, so ...

As you have described, imagine yourself standing on a contour line of the hill (a curve where height is constant). You want to go uphill as quickly as possible.

Imagine another contour line at a height that’s a tiny bit higher than the one you’re currently on. If “tiny” is small enough, the two contour lines will be almost parallel in the small region around your feet.

To go uphill as quickly as possible, you need to follow the shortest path from your current point to the higher contour. That shortest path between the two contour lines is in a direction that’s perpendicular to both of them.

Simple examples of a hill are a hemisphere or a cone with vertical axis. In both cases the two contour lines are circles, so the shortest path between them is pretty obvious.

bubba
  • 43,483
  • 3
  • 61
  • 122